 |
Моделирование
динамики популяций при помощи
клеточных автоматов.
"Жизнь"
("Эволюция") Д. Конвея |
Автором модели клеточной
популяции, известной под названием
"Жизнь", является английский математик Джон Хортон
Конвей, работавший над теорией
групп и клеточных автоматов. Динамика
популяции в ней определяется только
лишь процессами рождения и смерти
клеток. Они рождаются
- при благоприятном сочетании соответствующих факторов и умирают -
когда условия их существования становятся невыносимыми. Условия
рождения и умирания определяются исключительно взаимным расположением
участников, а правила игры жестко определяют, где и когда происходят
"рождение" и "смерть". Процесс эволюции происходит на бесконечном поле,
разделенном на
квадратики. Каждая ячейка игрового поля может находиться в двух
состояниях - либо оставаться пустой, либо быть занятой
живым организмом, клеткой. Смена поколений имитируется
в виде "циклов жизни", или из последовательности шагов. Переход от предыдущего
поколения к следующему происходит по правилам, которые
применяются одновременно ко всем клеткам:
|
Выживание
|
Клетка выживает
и переходит в следующее поколение, если рядом с ней заняты другими
клетками 2 или 3 соседние
ячейки.
|
|
Гибель
|
Клетка погибает в случае, если рядом занято
более трех или
менее двух соседних ячеек (в первом случае
- от перенаселения, во втором - от
одиночества).
|
|
Рождение
|
Если пустой квадрат поля граничит ровно с тремя
ячейками, занятыми клетками, то в нем происходит рождение нового "организма",
т.е. в следующем поколении на этой
ячейке появится новая клетка.
|
Эти правила относятся всегда к
состоянию, которое существует к началу "сезона". Все изменения
а популяции происходят как бы одновременно: определяется, на каких
ячейках будет происходить рождение и какие
клетки в следующей генерации вымрут. Затем происходит
смерть и рождение клеток - старая популяция
сменяется новой.
Любой объект, группа клеток, популяция, начав эволюционировать в начале Игры, в какой-то момент
прекращает свою эволюцию. Проявляется это в следующем:
-
популяция может полностью
выродиться (игровое поле очищается);
-
популяция может
деградировать к некоторому сочетанию стабильных объектов;
-
популяция
(кроме стабильных объектов) содержит также и пульсирующие объекты
- периодически повторяет свое состояние,
пульсирует.
Возможные варианты
стабильных и пульсирующих популяций, а
также структуры, способные мигрировать,
и другие интересные аспекты эволюции
клеточных популяций можно прочесть на сайте
Истинного
жизнелюба В.
Скляра. Или попробовать
создать свою популяцию клеток на поле
(:-(, не бесконечном) ниже. Нажатием левой
кнопки мыши на квадратиках поля Вы
создаете исходную популяцию, а потом
- запускаете ее процесс эволюции, нажав
на "START" (эта же кнопка в левом
верхнем углу после нажатия превратится
в "STOP");
- наблюдаете процесс смены поколений шаг
за шагом, поSTEPенно (нажимая на кнопку "STEP").
Успешной эволюции Вашим
популяциям!
Программы,
моделирующие эволюцию популяций клеток,
можно скачать бесплатно c ряда сайтов,
например, с сайта Антона
Дубины, а также с http://freeware.ru/.
Особенно удачна с точки зрения
программирования версия Life
32 (536 кб в zip-архиве, хотя
есть проблемы корректности работы
из-под Windows 2000), есть также программа Win_Life
(169 кб в zip-архиве).
 На принципе клеточных автоматов в более сложной
версии (ячейки по-прежнему зависят в своем
поведении от состояния соседних клеток, но могут
принимать разные значения, не только 1 или 0)
строятся сложные интерактивные модели.
На принципе клеточных автоматов в более сложной
версии (ячейки по-прежнему зависят в своем
поведении от состояния соседних клеток, но могут
принимать разные значения, не только 1 или 0)
строятся сложные интерактивные модели.
 1.
Волки, кролики и капуста ("Физикон",
"Открытая коллекция. Биология, 9 класс",
слева): по введенным в полях ввода
характеристикам определяется изначальное
количество и скорость размножения каждой из
популяций, однако судьба отдельный "особей"
зависит от соседей (см. разработку урока
"Биотические факторы. Межпопуляционные
взаимодействия", включающую работу с
этой моделью). 1.
Волки, кролики и капуста ("Физикон",
"Открытая коллекция. Биология, 9 класс",
слева): по введенным в полях ввода
характеристикам определяется изначальное
количество и скорость размножения каждой из
популяций, однако судьба отдельный "особей"
зависит от соседей (см. разработку урока
"Биотические факторы. Межпопуляционные
взаимодействия", включающую работу с
этой моделью).
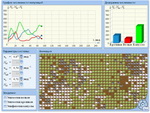
 2.
Стратегия отношений с сородичами по Докинзу
("Квазар-Микро", ИУМК
"Экология. Конструирование биосферы",
справа): в
модели множество сородичей представлено
полем 20*20 клеточек, на котором происходит
накопление ими жизненных бонусов и смена
организмов. Организмы могут кооперироваться с
соседями или отказываться от кооперации, при
принятии решения они не знают, будут ли соседи
кооперироваться с ними или отказываться, при
этом организмы различаться по жизненным
стратегиям (быть расположенными кооперироваться
или отказываться от кооперации, быть
злопамятными и т. п.). 2.
Стратегия отношений с сородичами по Докинзу
("Квазар-Микро", ИУМК
"Экология. Конструирование биосферы",
справа): в
модели множество сородичей представлено
полем 20*20 клеточек, на котором происходит
накопление ими жизненных бонусов и смена
организмов. Организмы могут кооперироваться с
соседями или отказываться от кооперации, при
принятии решения они не знают, будут ли соседи
кооперироваться с ними или отказываться, при
этом организмы различаться по жизненным
стратегиям (быть расположенными кооперироваться
или отказываться от кооперации, быть
злопамятными и т. п.). |
| |
|
    |