

 Серия:
«След вдохновений и трудов упорных…» Приложение к журналу
Серия:
«След вдохновений и трудов упорных…» Приложение к журналу
«Известия
вузов. Прикладная нелинейная динамика»
![]()
А.П.Кузнецов
Динамические системы и бифуркации
ООО Издательский центр «Наука»
Саратов
2015
УДК 517.91, 517.938, 51.73, 534.01
Кузнецов А.П.,
Динамические системы
и бифуркации – Саратов: ООО Издательский центр
«Наука», 2015, 168 с.
Учебно-научное издание
Представлено введение в теорию динамических систем и
бифуркаций. Обсуждаются свойст- ва основных бифуркаций. Даны различные примеры.
Изложение ведется с «физических» позиций, так что выбираются простейшие модели,
для которых проводится комплексное рас- смотрение, включая аналитический поиск
бифуркаций, иллюстрации в виде карт динамиче- ских режимов и карт ляпуновских
показателей и т.д. Будет полезна студентам, аспирантам и преподавателям как
пособие в области нелинейной динамики и теории динамических сис- тем.
Использованы материалы, полученные при выполнении гранта Президента РФ поддержки ведущих научных школ России НШ-1726.2014.2 и РФФИ проект 14-02-00085.
ISBN 978-5-9999-2335-6
Рекомендуют к печати:
Базовая кафедра динамических систем Саратовского государственного университета им. Н.Г. Чернышевского.
Рецензенты:
д.ф.-м.н., проф. Кузнецов С.П.
к.ф.-м.н. Сатаев И.Р.
Ó Кузнецов А.П.
Оригинал-макет подготовлен автором
ISBN 978-5-9999-2335-6
Предисловие........................................................................................... 4
Часть I. Динамические системы.............................................................. 5
Динамические системы. Примеры и простейшие свойства.................. 6
Конструирование отображений............................................................ 13
От потоков к отображениям: метод медленно меняющихся амплитуд…31
Часть II. Бифуркации потоков............................................................... 43
Бифуркации одномерных потоков........................................................ 44
Бифуркации двумерных потоков.......................................................... 49
Бифуркации трехмерных потоков........................................................ 79
Компьютерное исследование трехмерных потоков.............................. 95
Размерность четыре............................................................................ 101
Часть III. Бифуркации отображений..................................................... 103
Бифуркации одномерных отображений коразмерности один............ 104
Бифуркации двухпараметрических
одномерных отображений................................................................... 118
Двумерные отображения и их бифуркации......................................... 124
Трехмерные отображения и их бифуркации........................................ 142
Бифуркации инвариантных кривых (торов)…..................................... 151
Задачи для компьютерного практикума.............................................. 159
Мир динамических систем очень разнообразен. К ним относятся механиче-
ские, радиофизические, электронные, оптические, химические и другие систе- мы. Такая общность возникает благодаря единству математического аппарата, представляющего собой теорию
динамических систем и теорию бифуркаций. Следствием этого междисциплинарного взаимодействия явилось возникновение
соответствующих разделов математики. С
другой стороны, важными являются приложения в различных областях науки. В настоящей книге излагается взгляд физика
на соответствующие вопросы. По этой причине мы отталкиваемся не от математических теорем, а от физических
постановок задач, например, о разно-
образных осцилляторах. Это своего рода индуктивное построение изложения
материала, однако, оно более удобно для практических целей.
Отметим, что для динамических систем и бифуркаций характерна, по вы- ражению В.И.Арнольда, «тонкая игра дискретного и непрерывного», что мы старались отразить в настоящем пособии.
В качестве формы изложения материала выбраны задачи. Это удобно по следующим причинам. Во-первых, дает возможность читателю самостоятельно попробовать разобраться в соответствующих вопросах. Кроме того, возникает возможность, поэтапно решая задачи, продвигаться вперед «шаг за шагом», четко фиксируя результаты каждого такого шага.
В основу книги положен курс лекций «Динамические системы и бифурка- ции», разработанный автором для Факультета нелинейных процессов Саратов- ского государственного университета. Со временем курс развивался и допол- нялся.
Автор выражает благодарность С.П.Кузнецову и И.Р.Сатаеву за полезное обсуждение и Ю.В.Седовой, Н.В.Станкевич, А.В.Савину и Л.В.Тюрюкиной за помощь.
Динамические системы. Примеры и простейшие свойства
1.
Продемонстрируйте свойства гармонического осциллятора
&x& + w2 x = 0
0
как динамической системы. Для этого
найдите матрицу эволюции, позволяю-
щую определить вектор-столбец, составленный из величин x(t) и
x&(t) , в любой
момент времени по его начальному значению. Вычислите определитель этой
матрицы и
прокомментируйте полученный результат. Здесь
w0
частота осциллятора.
– собственная
Решение 1. Решая дифференциальное уравнение гармонического осцилля-
тора с начальными условиями рости от времени
x0 , x&0 , получим зависимости координаты и ско-
x(t) =x0
cosw0t +
x&0
![]() w0
w0
sin w0t,
x&(t) = -w0 x0 sin w0t +
x&0 cosw0t.
В матричной форме эти соотношения можно записать следующим образом:
x(t)
æcosw t
1 sin w t ö x
![]()
æ ö ç 0
w 0 ÷æ 0 ö
ç x&(t) ÷ = ç
0 ÷ç x& ÷.
è ø ç- w
sin w t
cosw t
÷è 0 ø
è 0 0 0 ø
Полученная матрица и задает оператор эволюции, позволяющий опреде- лять состояния системы в любой момент времени по начальному состоянию.
Вычисляя определитель этой матрицы, получаем
J = 1. Поскольку определи-
тель отвечает за сжатие (расширение) элементарных площадок на фазовой пло- скости, то получаем, что рассматриваемая система является консервативной. Для нее элементарные площадки не меняют своей площади.
2.
Решите аналогичную задачу для осциллятора с затуханием
0
&x& + 2ax& + w2 x = 0 , где параметр
затухания
a < w0
. Найдите якобиан соответст-
вующей матрицы и обсудите свойства сжимаемости на фазовой плоскости.
Решение 2. Решая соответствующее дифференциальное уравнение для ос-
циллятора с затуханием при
a < w0
с начальными условиями
x0 , x&0
можно по-
лучить следующие зависимости координаты и скорости от времени:
è ø
x(t) = æ x coswt +
x&0 + ax0 sin wt öе-at
,
![]()
ç 0 w ÷
æ
x&(t) = ç-
è
(a2 +
w2 )x0 +ax&0
![]() w
w
ö
sin wt + x&0 coswt ÷e
ø
-at ,
где w =
w2 - a2 .
В матричном виде эти соотношения можно переписать сле-
0![]()
дующим образом:
æcoswt + a sinwt
![]()
1 sin wt ö
![]()
æ x(t) ö -a ç w w
÷
x t ÷ x&
æ 0 ö
ç ÷ =
e
t ×ç
÷ç ÷.
è x&(t) ø
ç a2 + w2
-
ç
sin wt
coswt
- a sin w
ç
÷è 0 ø
![]()
è w w ø
Таким образом, мы получили оператор эволюции системы в явном виде.
Вычисляя якобиан этой матрицы, получаем
J = e-at . Поскольку параметр дис-
сипации
a > 0 , то якобиан меньше единицы. Это означает, что система дисси-
пативна, и небольшая площадка на фазовой плоскости с течением времени сжимается. Скорость сжатия управляется параметром затухания осциллятора.
3. Простейший
генератор электромагнитных колебаний, содержащий ак- тивный элемент в виде
электронной лампы или транзистора, описывается урав- нением Ван дер Поля
&x& -
(l -
x2
)x& +
x = 0.
Представьте это уравнение в «стандартной» для динамической системы форме. Рассмотрите также случай неавтономной системы с внешним воздействием:
&x& -
(l -
x2
)x& +
x = Asin
wt.
Решение 3. Уравнение двумерной и трехмерной динамической системы в стандартной форме имеет вид:
x& = f (x, y),
x& = f (x, y, z),
y& = g(x, y),
y& = g(x, y, z),
z&
= v(x, y, z).
Выполним в исходном уравнении Ван дер Поля
&x& -
(l
- x2 )x& +
x = 0
заме-
ну переменной
y = x& .Тогда оно приводится к стандартному виду:
x& =
y,
y& = (l - x2
) y - x.
В случае неавтономной системы необходимо ввести третью переменную
z = wt . Тогда получаем
x& = y,
y& = (l - x2 )
y
- x + Asin z, z& = w.
Таким образом, систему Ван дер Поля с внешним сигналом можно рас- сматривать как трехмерную динамическую систему.
Отметим, что значение уравнения Ван дер Поля выходит за рамки описа- ния электронных генераторов – оно является универсальной моделью автоколе- баний для систем различной физической природы.
4.
Одной из первых систем,
для которой был обнаружен динамический ха-
ос,
являлась простая модель тепловой конвекции в атмосфере – система Ло- ренца:
x& = s(y
- x),
y& = rx - y - xz, z& = xy - bz.
Здесь s, r, b — параметры. Установите значения параметров, при которых мо- дель Лоренца является диссипативной.
Решение 4. Уравнения трехмерной потоковой системы задают в фазовом
пространстве
(x, y, z)
некоторое векторное поле:
V ( f (x, y, z), g(x, y, z), v(x, y, z)) .
Вычисляя дивергенцию этого поля div V = f ¢ + g¢ + v¢ , можно судить о его
x y z
сжимаемости. Вычисляя соответствующие частные производные для системы Лоренца, получаем
div V = -s -1 - b.
Таким образом, поток является сжимающим, если div V <0, так что систе- ма диссипативна, если
s + 1 + b > 0 .
5.
Белоусовым и Жаботинским была
открыта колебательная химическая реакция,
в ходе которой раствор периодическим образом меняет цвет. Филд и Нойес предложили
упрощенную схему этой реакции, модель, которую называ- ют орегонатором:
k1
A + Y ® X ,
k 2
X + Y ® P,
B + X
k 3
® 2 X + Z ,
k 4
2 X ® Q,
k 5
Z ® fY .
Здесь ki
–
коэффициенты, отвечающие за скорость
соответствующего процес-
са, A и B – исходные реагенты, P и Q – продукты реакции, X, Y, Z – проме- жуточные соединения. Получите динамическую систему для переменных X, Y, Z, описывающую эту реакцию.
Решение 5. Необходимо написать соответствующие кинетические уравне- ния1. Они определяют скорости изменения переменных в соответствии со схе- мой реакции. В данном случае имеем:
x& = k1 Ay - k2 xy + k3 Bx - 2k4 x2 ,
y& = -k1 Ay - k2 xy +
z& = k3 Bx - k5 z.
fk5 z,
В безразмерной форме нетрудно получить
x& = s(
y -
xy +
x -
qx2
), 1
![]() y& = s (- y - xy + fz),
y& = s (- y - xy + fz),
z& = w(x
- z).
Приведем типичные значения параметров: s=77.27,
q = 8.375 ×10-6 ,
w = 0.161×k 5 ,
0 <k 5< 1,
0 < f
< 2.
Замечательная особенность кинетических уравнений состоит в том, что получаются соотношения, отвечающие стандартной форме для динамической системы. В частности, это явилось одним из мотивов построения Ресслером це- лой «коллекции» модельных уравнений.
6. Найдите
матрицу возмущений, описывающую эволюцию малых элемен- тов на фазовой
плоскости, для отображения типа Эно
xn+1=
f (xn ) - byn ,
yn+1 = xn .
Из ее вида установите, когда это отображение консервативно, а когда дис-
сипативно. Зависит ли это от вида функции бражение обратимо.
f (x)? Покажите, что данное ото-
Решение 6. Если динамическая система на плоскости задана в общем виде
x& =
f (x, y),
y& = g(x, y),
то эволюция
малых элементов dx и dy происходит в соответствии с матрицей возмущений (матрицей Якоби)
æ f x¢
Мˆ = ç g¢
f y¢ ö
g¢ ÷ .
è x y ø
1 При этом используется так
называемый «закон действующих масс». Подробнее см. Коле- бания и бегущие волны
в химических системах. М.: Мир, 1988, с. 168-169.
Для отображения типа Эно, вычисляя соответствующие частные производ- ные, получаем
ˆ æ f ¢(x) -
b ö
М =
ç ÷
.
è 1 0 ø
Якобиан матрицы Мˆ равен
J = b
и не зависит от фазовых переменных.
Таким образом, это отображение относится к классу отображений с постоян-
ным якобианом. Оно диссипативно
при
b <
1
и консервативно при
b = 1. Эти
свойства не зависят от вида функции f (x).
Уравнения, задающие отображение типа Эно, можно переписать в виде
xn = yn+1,
yn =
f ( yn+1) -xn+1 .
![]() b
b
Таким образом, получено выражение для значений переменных от их значений на последующем шаге. Это означает обратимость такого отображения.
7.
Предлагается следующая
классификационная схема построения эталон- ных модельных отображений:
·
n
линейное отображение
xn+1 = l + xn ;
· логистическое отображение
xn+1
= l- x2 ;
· кубическое отображение
· …
xn+1
= a + bx
± x3;
n n
Продолжите этот ряд, минимизируя на
каждом шаге число существенных параметров с помощью замен в виде сдвига
динамической переменной и пере- нормировки переменной и параметров. Сравните
такой анализ с подходом тео- рии
катастроф.
Решение 7. Пусть имеется отображение
общего вида
xn+1 =
f (xn ) . Для по-
строения системы моделей можно использовать разложение в ряд Тейлора
систему координат в эту точку. Тогда
y = f
+ f ¢ × x +
1 f ¢ ×
x2
+ 1
![]()
![]()
f ¢¢× x3 + 1 f IV × x4 + ... + 1
![]()
f (n) xn + ...
0 0 2 0
6 0 24 0
![]()
n! 0
Здесь
f0 – значение функции в начале координат, а
f0¢,.
f0¢, f0¢¢
и т.д. –
производные, вычисленные в этой точке.
2 При этом функция должна, строго
говоря, удовлетворять некоторым условиям, например, не
иметь разрывов. Для нас здесь достаточно интуитивного представления о
«гладкости» функции.
Чем больше членов ряда Тейлора сохранить, тем более точно описывается функция в окрестности начала координат. Этот факт имеет простой геометри-
ческий смысл. Если сохранить только линейный член, т.е.
y = f0 +
f0¢ × x + .... , то
мы заменяем функцию касательной. Если удержать члены до квадратичного включительно, то функция аппроксимируется более точно – квадратичной па- раболой. Если удержать кубический член, то аппроксимация станет еще более точной. Одновременно расширяется область, в которой аппроксимация эффек- тивна.
Оставим сначала только линейный член:
xn+1 =
f0 +
f0¢ × xn .
Изменяя масштаб переменной в
лучаем линейное
отображение:
f0¢ раз и вводя обозначение l =
f0 / f0¢ , по-
xn+1 = l + xn .
Учтем следующий член ряда Тейлора:
x =
f
+ f ¢ × x
+ 1 f ¢ × x2 .
![]()
n+1
0 0 n
2 0 n
Мы
получили квадратичное отображение, в
которое входит уже три ко- эффициента, которые удобно обозначить через A,B,C:
n
xn+1 = A + Bxn + Cx2 .
Заменой переменной типа сдвига член. В результате получаем:
x ® x - B
![]() 2C
2C
можно устранить линейный
где
D = A + B
![]() 2C
2C
- B 2
![]()
4C
xn+1 = D + Cx2
,
n
. Теперь изменим масштаб переменной, так что
x ® ax :
x = D + Cax 2 .
![]()
n+1 a n
Подбором параметра a = -1/ C
это отображение приводится к виду
n
xn+1 = l - x2 ,
где l = -CD . Таким образом, мы получили логистическое отображение3.
Такой анализ можно продолжить, и удержать кубический член ряда:
x =
f
+ f ¢ × x + 1 f
¢ × x2 + 1 x3 ,
![]()
![]()
n+1
0 0 n 2 0 n 6 n
или
n n
xn+1 = A + Bxn + Cx2 + Dx3 .
Заменой типа сдвига
x ® x -
C устраняем
квадратичный член: 3D
n![]()
xn+1 = E + Gxn + Dx3 .
Здесь
E = A - BC
![]() 3D
3D
2C 3
+![]()
,
27D 2
G = B - C
2![]()
3D
. Затем изменяем масштаб переменной
x ® ax :
x = E + Gx + Da2x3
.
![]()
n+1 a n n
![]() Если выбратьa = 1
Если выбратьa = 1
и ввести обозначения
a = E
![]() D , b = G , то приходим
D , b = G , то приходим
к кубическому
отображению
n
xn+1=a + bxn ± x3 .
Отметим, что «спрятать» знак перед кубическим членом нельзя, потому
![]() что переменная x нормируется
на величину a =
что переменная x нормируется
на величину a =
1 , которая всегда положи-
тельна. При этом знак выбирается в соответствии со знаком D.
Теперь нетрудно уже просто «угадать» вид квартичного трехпараметриче- ского отображения:
n n
xn+1=a + bxn + cx2 + x4 .
Здесь следует сделать одно существенное замечание. Если исходная функ-
ция
f (x)
задана, то коэффициенты ряда Тейлора – это некоторые числа. Если
она зависит от параметра (параметров), то эти коэффициенты сами будут неко- торыми функциями этих параметров. Представленный здесь подход интересен в том плане, что можно рассматривать l или a, b и т.д. как новые параметры. При этом, если мы изучим поведение полученных отображений при всех их значениях, то мы, в определенной мере, получим полную картину явлений в одно-, двух-, трех и более параметрических отображениях. Такой подход заме- чателен тем, что позволяет понять универсальность получаемых результатов. В его рамках в рассмотрение вводится система универсальных моделей со все бо- лее сложным поведением, при этом возрастет число существенных параметров, от которого это поведение зависит. Это важный принцип теории бифуркаций. Минимальное для данного типа поведения число существенных параметров но- сит специальное название – коразмерность.
Нетрудно видеть, что описанная схема аналогична конструированию кано- нических одномерных моделей в теории катастроф. Приведем построенную систему моделей. В скобках указана терминология в соответствии с теорией катастроф.
·
xn+1 = l +
xn
·
n
xn+1 = l -
x2
–
линейное отображение,
–
логистическое отображение (складка),
·
n
xn+1 = a + bxn ±
x3
–
кубическое отображение (сборка),
·
n n
xn+1 = a + bxn + cx2 -
x4
–
квартичное отображение (ласточкин хвост),
·
n n n
xn+1 = a + bxn + cx2 + dx3 ±
x5
–
отображение пятой степени (бабочка) и т.д.
8.
Постройте аналогичный ряд для
двумерных отображений с постоянным якобианом.
Решение 8. Используя формулу
xn+1=
f (xn ) - eyn ,
yn+1 = xn ,
можно получить соответствующий ряд
многопараметрических двумерных ото- бражений. Первую строчку в такой
классификации для нелинейного случая бу- дет занимать отображение Эно
n
xn+1= l - x2 - eyn ,
yn+1 = xn .
Следующую строку занимает двумерное кубическое отображение
n
xn+1= a + bxn ± x3 - eyn ,
yn+1 = xn ,
которое иногда называют отображением Холмса и т.д.
9. Покажите, что отображение
1 æ a ö
è n ø![]()
![]()
xn+1 = 2 ç xn + x ÷ ,
можно использовать для вычисления квадратного корня из числа a. (Такой способ применяли еще в древнем Вавилоне). Для a=2 найдите первые пять чле-
нов последовательности
xn , порождаемых этим отображением, и сравните ре-
зультат с точным. Величину
x1 положите равной единице. Можно ли использо-
вать для вычисления квадратного корня отображение
xn+1 = ?
a x![]()
n
Решение 9. Проверим сначала эффективность алгоритма. Полагая
x1 = 1, получаем:
a = 2 и
![]() x2 = 1.5,
x2 = 1.5,
x3 = 1.41666...,
x4 = 1.41421...
Точное значение
= 1.41421...
Таким образом, алгоритм работает, и схо-
димость достаточно быстрая.
Обоснуем этот
результат. Итерационная процедура будет сходиться к не-
подвижной точке отображения, которую
ищем из уравнения
x0 =
f (x0 ) :
1 æ a ö
![]()
![]() x0 = 2 ç x0 + x ÷ .
x0 = 2 ç x0 + x ÷ .
![]() è 0 ø
è 0 ø
Таким образом
x0 =
a . Этого, однако, недостаточно – необходимо также, что-
бы точка была устойчивой. Для исследования на устойчивость вычисляем
мультипликатор в неподвижной точке:
m = f ¢(x0
) = 1 -
![]() 2
2
a
0![]()
2x2
= 0 .
Использованный итерационный алгоритм устойчив. Более того, поскольку мультипликатор равен нулю, то он характеризуется максимальной скоростью сходимости (сверхсходимостью).
Отображение
xn+1 =
a , хотя и имеет такую же неподвижную точку
![]() xn
xn
![]() x0 =
x0 =
, но характеризуется мультипликатором
m = f ¢(x0
) = -
a = -1, т.е. не
x 2![]()
0
подходит для реализации итерационного метода.
10.
Имеется бесконечная цепочка
сопротивлений, показанная на рис.1. По- лучите дискретное отображение,
позволяющее определить величину сопротив-
ления
xn+1
цепочки, составленной из n+1 звеньев, по величине сопротивления
xn цепочки из n звеньев. Сопротивления всех резисторов одинаковы и равны
1 Ом. Определите сопротивление бесконечной цепочки
x0 , найдя неподвижную
точку полученного отображения. Исследуйте ее устойчивость. Проиллюстри- руйте решение с помощью итерационной диаграммы в виде зависимости
xn+1 =
f (xn ).
Сколько элементов должна содержать цепочка, чтобы ее сопро-
тивление равнялось величине
x0 с точностью до 1%? Что измениться, если
крайнее правое сопротивление равно 100 Ом?
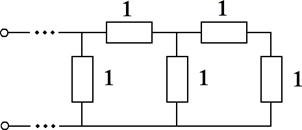
Рис.1.
Цепочка
сопротивлений.
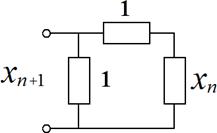
Решение 10. Эквивалентная схема для построения отображения приведена на рис.2.
Рис.2.Эквивалентная схема
цепочки сопротивлений.
n
По правилам расчета параллельного и
последовательного соединения рези- сторов получаем
x = f (x
) = xn +1 .
![]()
n+1
xn + 2
Это и есть искомое отображение. Итерационная диаграмма, иллюстрирующая
построение последовательности
xn с помощью графика
f (x), дана на рис.3.
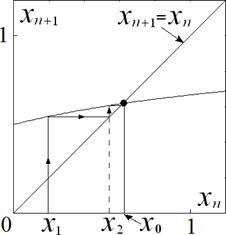
Рис.3. Итерационная диаграмма отображения для цепочки
сопротивлений.
Как видно из рисунка, отображение имеет неподвижную точку
x0 =
f (x0 )
,
отвечающую пересечению биссектрисы и графика функции. Отсюда следует ответ к задаче об определении сопротивления бесконечной цепочки:
x0 =
5 -1 = 0.618034... .
![]()
![]() 2
2
Необходимо еще проверить, является ли это решение устойчивым. Для этого вычисляем мультипликатор в неподвижной точке:
m = f ¢(x0 ) =
1
2 =![]()
![]()
![]()
(2 +
x0 ) (
4
+ 3)2
» 0.145900...
Таким образом, 0<μ<1. Это означает, что итерации сходятся, причем весь-
ма быстро, поскольку мультипликатор m = f ¢(x0 ) мал. В этом несложно убе- диться, итерируя отображение.
|
Число звеньев в цепочке, n |
xn |
Отклонение от не- подвижной точки, % |
|
1 |
x1=1 |
|
|
2 |
x2=2/3»0.666667 |
7.86 |
|
3 |
x3=5/8»0.625000 |
1.12 |
|
4 |
x4=13/21»0.619048 |
0.16 |
|
5 |
x5=34/55»0.618182 |
0.02 |
|
… |
… |
… |
|
¥ |
x0= 5 - 1
» 0.618034 2 |
0 |
![]() Из таблицы видно, что, цепочку всего из трех звеньев можно считать
«бес-
Из таблицы видно, что, цепочку всего из трех звеньев можно считать
«бес-
конечной» с точностью почти до 1%, а из пяти – уже с точностью до 0.02%.
Если начальное значение x1 изменить, то все равно процесс будет сходить- ся к неподвижной точке в силу ее устойчивости, просто понадобится несколько большее число итераций. При этом сходимость очень быстрая, например, для x1=100 получаем x2=0.9902…, x3=0.6657…, x4=0.6249 и т.д.
![]() Отметим, что неподвижная точка данного отображения отвечает так назы-
Отметим, что неподвижная точка данного отображения отвечает так назы-
![]() ваемому золотому сечению
ваемому золотому сечению
5 -1 , наиболее удобному для исследований ирра- 2
циональному числу, а последовательность
xn во втором столбце таблицы отве-
чает его рациональным апроксимантам с помощью
чисел Фибоначчи
Fn :
F n![]()
x = F2n-1 , которые сами получаются с
помощью итерационной процедуры:
2n
Таким образом,
Fn+1 = Fn + Fn-1 , причем F0 = 0, F1 = 1.
F0 = 0, F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8,
...
Сравните приведенную последовательность с данными таблицы 1.
11.
Тенисон, Либерман и Лихтенберг
рассмотрели следующую систему: луч света может бежать между двумя зеркалами, одно из которых имеет «гоф-
рировку» в виде гармонической функции
y(x)
= h + a cos kx , рис.4. Здесь a – ам-
плитуда гофрировки, h – среднее расстояние между зеркалами. Получите дву- мерное дискретное отображение, описывающее динамику этой системы, считая гофрировку слабой. В качестве переменных используйте угол падения луча на
нижнее зеркало jn
и координату
xn падения луча на верхнее зеркало.
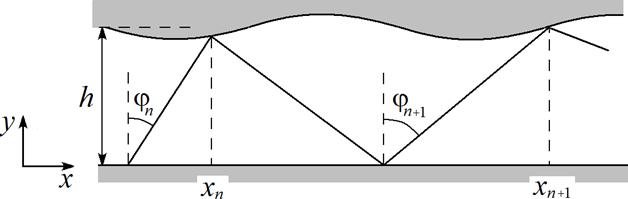
Рис.4. Луч
света, распространяющийся между двух отражающих поверхностей и перемен- ные для
построения отображения.
Решение 11. Пусть луч падает на гофрированное зеркало в точке с коорди-
натой
xn . Считая гофрировку слабой, несложно найти угол a наклона зеркала в
этой точке. Действительно, при малых углах
tga » a. В свою очередь,
tga
» y¢(x) =
-ak
sin kx ,
и для точки
xn имеем
a = -ak sin kxn .
Пусть луч падает на верхнее зеркало в точке О, рис.5. Построим нормаль в этой точке ON. Угол между падающим на верхнее зеркало лучом и нормалью
будет равен
jn+1 = jn + a .
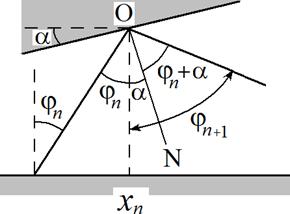
Рис.5. Отражение луча
света от гофрированной поверхности.
Из геометрического построения на рис.5 и правила «угол падения равен углу отражения», получаем, что луч отражается от верхнего зеркала под углом
jn + 2a . Этот же угол отвечает следующему падению луча на нижнее зеркало,
поэтому ясно, что
jn+1 = jn + 2a . Кроме того, из геометрических соображений и рис.5
(xn+1 - xn ) = 2htgjn+1. Собирая результаты вместе, получаем двумерное
отображение
jn+1 = jn - 2ak sin kxn ,
xn+1 = xn + 2htgjn+1.
Вместо координаты x удобно ввести безразмерную фазовую переменную
q = kx . Тогда
получаем искомое отображение Тенисона,
Либермана и Лихтен- берга:
jn+1 = jn - 2ak sin qn ,
qn+1 = qn +
2hktgjn+1.
Отметим, что обе фазовые переменные следует брать по модулю 2π. С точ- ки зрения переменной q это означает, что рассмотрение ведется в пределах од- ного периода синусоиды гофрировки. (Луч, переходя в следующий отрезок волновода, как бы попадает снова на тот же участок, но уже с противоположной стороны.)
Полученное отображение характеризуется двумя безразмерными парамет- рами, имеющими смысл амплитуды гофрировки ak и расстояния между зерка- лами hk . Нетрудно показать, что якобиан отображения точно равен единице, так что оно является консервативным. Это понятно и из физических соображе- ний. (При вычислении якобиана обратите внимание, что во второе уравнение
входит член с
jn+1 .)
12.
Получите отображение
Улама для механической системы, являю- щейся моделью ускорения Ферми,
рис.6. Стенка колеблется так, что ее скорость
изменяется по гармоническому закону V (t ) = V0 sin wt. Смещением стенки пре-
небречь, расстояние между стенками L. Все удары упругие.
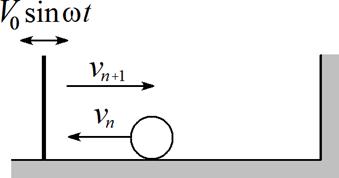
Рис.6.
К
построению модели Улама.
Решение 12. Поместим начало координат в точку положения вибрирую- щей стенки. (Ее смещениями пренебрегаем.) Пусть скорость шарика перед n-ым
ударом об эту стенку равна
vn . Перейдем в систему отсчета, связанную со стен-
кой. В этой системе отсчета шарик налетает на стенку со скоростью
vn + V0 sin wt . При ударе по условию задачи шарик теряет долю скорости, про- порциональную величине e. Тогда в этой системе отсчета скорость шарика по-
сле n-го удара будет равна (1 - e)(vn + V0 sin wtn ) и изменит направление. Вер-
немся в исходную систему отсчета, и находим скорость шарика после удара
(1- e)(vn +
V0 sin wtn )+ V0 sin wtn . Нетрудно видеть, что это же значение
отвечает
скорости шарика перед (n+1)-ым ударом, так что
vn+1 = (1- e)vn + (2 - e)V0 sin
wtn .
Мы пока не получили замкнутую систему уравнений, поскольку искомое отображение должно быть двумерным. В качестве второй переменной удобно
выбрать момент
времени tn
столкновения шарика со стенкой. После удара о
подвижную стенку шарик движется равномерно со скоростью соударение с подвижной стенкой произойдет через время
vn+1 . Очередное
2L / vn+1 . Тогда
tn+1 = tn + 2L / vn+1 . Собирая результаты вместе, получаем двумерное отображе-
ние:
tn+1 = tn + 2L / vn+1,
vn+1 = (1- e)vn + (2 - e)V0 sin
wtn .
Обратите внимание, что в первое уравнение нужно подставлять проитериро- ванное второе.
Отображение можно упростить, вводя безразмерные время (фазу)
скорость шарика u = v / 2Lw:
j = wt и
Здесь
jn+1 = jn +1/ vn+1 (mod 2p),
un+1 = bvn + k sin wtn .
![]() k = (2 - e)V 0 –
безразмерный параметр, характеризующий амплитуду
k = (2 - e)V 0 –
безразмерный параметр, характеризующий амплитуду
2wL
колебаний стенки,
b =
1 - e
–
параметр затухания. Символ mod 2π означает сно-
ва, что полученное значение фазы нужно «вернуть» на интервал
0 < j < 2p, от-
бросив часть 2πm, где m – целое число. Это вполне естественно, так как по фи- зическому смыслу φ является фазой колебаний плиты, а отличающиеся на 2π значения фазы физически неразличимы4. Это отображение называют отобра- жением Улама.
Рекомендуем самостоятельно вычислить якобиан этого отображения и по-
казать, что при
0 < e < 1 оно диссипативно, а при
e = 0
–
консервативно.
Заметим, что
скорость vn
должна быть всегда положительной, поскольку
только в этом случае происходит столкновение со стенкой, смещением которой можно пренебречь. Однако полученное отображение может демонстрировать и
«нефизические» решения с отрицательной скоростью. Тем не менее, часто рас- сматривают и этот случай, считая такую модель отчасти формальной. Иногда ее
«подправляют», беря значения скорости по абсолютной величине:
jn+1 = jn +1/ vn+1 (mod 2p),
![]()
![]() un+1 = bvn + k sin wtn .
un+1 = bvn + k sin wtn .
13.
Постройте «отображение прыгающего
шарика» – решите аналогичную задачу в случае горизонтально расположенного
вибрирующего стола, рис.7.
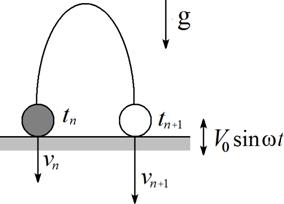
Рис.7. К построению отображения «прыгающего шарика».
![]()
4 Далее в целях
сокращения записи соответствующий значок будем опускать.
Решение 13. Решение задачи аналогично предыдущей, отличие состоит
лишь во времени, необходимого для возврата шарика:
В результате получаем отображение
tn+1 = tn + 2vn+1 / g,
2vn+1 / g вместо
2L / vn+1.
vn+1 = (1- e)vn + (2 - e)V0 sin
wtn .
Вводя безразмерные величины
j = wt , u = 2wv / g
jn+1 = jn + vn+1 ,
и k = 2w(2
- e)V 0 , получаем:
![]() g
g
un+1 = bvn + k sin jn .
Это отображение
прыгающего шарика. В более общем контексте его на- зывают диссипативной
версией стандартного отображения (см.
задачу 16).
14.
Пусть имеется система, движущаяся в
вязкой среде под действием пе- риодической последовательности коротких
импульсов большой амплитуды, ко- торые можно заменить последовательностью
дельта-функций. Величина им-
пульса зависит от координаты тела в соответствии с некоторой функцией
¥
f (x)
:
&x& + ax& =
f (x)åd(t - nT ).
-¥
Нарисуйте качественно траекторию на фазовой плоскости
(x, x&) . Укажите
точку
xn , x&n
сразу после n-го импульса, момент и результат действия очередно-
го (n+1)-го импульса и точку
xn+1, x&n+1. Получите аналитически соответствую-
щее отображение для данной системы. Обсудите частный случай постоянной амплитуды C. Имеет ли отображение неподвижные точки? Приведите его к безразмерному виду и покажите, что оно приводится к отображению типа Эно.
Указания. Если сила зависит от времени в соответствии с дельта-функцией
Сd(t) , то в результате импульса координата тела не меняется, а скорость воз- растает на величину C. Для того, чтобы выполнить последнее задание, удобно представить отображение для координаты через скорость в (n+1)-ый момент времени.
Решение 14. Сначала дадим качественную иллюстрацию динамики на фа- зовой плоскости. Фиксируем начальный момент времени непосредственно пе-
ред n-ым импульсом. Координата и скорость равны мики системы и выбора переменных дана на рис.8.
xn , vn . Иллюстрация дина-
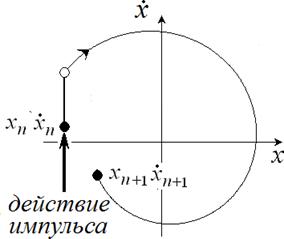
Рис.8. Эволюция
системы двумерной динамической системы под действием импульса на фазовой
плоскости. Белым кружочком показано «промежуточное» значение.
Действие дельта-образного импульса приводит к тому, что координата не
меняется, а скорость получает добавку, равную амплитуде импульса
f (xn ) . Та-
ким образом, сразу после импульса координата будет равна
xn , а скорость ста-
нет равна
vn +
f (xn ).
Полученное в результате положение изображающей точки
показано на рис.8 белым кружочком.
Далее, в промежутке между импульсами, эволюция происходит в соответ-
ствии с автономным уравнением
&x& + ax& = 0.
Решая его, получаем зависимость
координаты и скорости от времени:
![]() x(t) = x(0) + v(0) (1- e-at ), v(t) = v(0)e-at ,
x(t) = x(0) + v(0) (1- e-at ), v(t) = v(0)e-at ,
a
где в качестве начальных значений следует использовать
xn и
vn +
f (xn ). Теперь
можно найти координату и скорость к моменту (n+1)-го импульса:
1 - e-aT
![]() xn+1 =xn +(vn + f (xn )) a ,
xn+1 =xn +(vn + f (xn )) a ,
vn+1= (vn +
Это и есть искомое отображение.
f (xn ))e-aT .
В частном случае импульсов постоянной амплитуды C получаем закон из- менения координаты и скорости
xn+1 =xn +(vn + С)
1- e-aT
![]() a ,
a ,
vn+1= (vn + С)e-aT .
В этом случае получаем некоторую установившуюся среднюю скорость
v0 =
C
![]()
eaT -1
. Координата же будет неограниченно нарастать, стремясь к асим-
птотическому закону x
=x + nС . Таким образом, при
![]()
f ( x) = С
неподвижной
точки нет.
n+1 1 a
В общем случае неподвижная точка отображения определяется из условий
v0 = 0,
f (x0 ) = 0.
Физически это отвечает нулевой скорости в точке, для которой
импульс внешней силы равен нулю.
Приведем отображение к безразмерному виду. Перенормируя скорость по
правилу
y = v (eaT -1)
![]() a
a
и соответствующим образом функцию
f (x) , получаем:
xn+1 =xn +e( yn + f (xn ),
yn+1= e( yn + f (xn )),
где
e = e-eT
–
параметр диссипации. Нетрудно показать, что якобиан
этого ото-
бражения
J = e , так что оно является диссипативным при
g > 0
и консерватив-
ным при
g = 0 , что ясно и из физических соображений.
Следуя условию задачи, замечаем, что отображение можно представить также в виде
xn+1 =xn + уn+1,
yn+1= e( yn + f (xn )).
Из первого уравнения видно, что удобно ввести переменную
Тогда:
Yn =xn - уn .
где
Yn+1 =xn ,
xn+1= F (xn ) - eYn ,
F (x) = (1 + e)x + ef (x) .
Таким образом, система приводится к отображению
типа Эно.
15.
Рассмотрите ротатор – вращающийся маятник с затуханием с нуле- вой собственной
частотой – под действием внешнего сигнала, представляющего собой постоянный
вращательный момент M и импульсную
силу, создающую дополнительный вращающий момент:
¥
&x& + ax& = M + e sin xåd(t - nT ) .
-¥
Покажите,
что такая система приводится к двумерному отображению
кольца
xn+1 = xn + W + k sin xn + brn ,
rn+1 = br + k sin xn .
Укажите физический смысл безразмерных параметров в этом отображе- нии. Рассмотрите частные случаи сильной и нулевой диссипации.
Решение 15. Решение задачи аналогично предыдущей. Отличие состоит в динамике системы в промежутке между импульсами. В этом случае уравнение
&x& + ax& = M имеет решение
æ M ö 1-e-at M
![]()
![]()
![]() x(t) = x(0) + ç v(0) - ÷
x(t) = x(0) + ç v(0) - ÷
è a ø a
+ a t,
v(t)
= æ v(0) - M öe-at + M .
![]()
![]()
ç ÷
a a
è ø
Соответственно, отображение имеет вид:
æ M ö 1-e-aT M
![]()
![]()
![]() xn+1 = xn + ç vn + e sin xn - ÷
xn+1 = xn + ç vn + e sin xn - ÷
è a ø a
+ a T ,
v = æ v
+
e sin x
- M öe-aT + M .
![]()
![]()
n+1 ç n
è
n a ÷ a
ø
Удобно ввести переменную
y = v - M ,
![]() a
a
характеризующую скорость во
вращающейся системе отсчета. Тогда
xn+1 = xn + (yn + e
sin xn )
1-e-aT
![]() a
a
+
M T ,
![]() a
a
yn+1 = (yn + e sin xn )e-aT .
Вводя переменные и параметры
eaT -1
![]() r = a
r = a
y, b = e
-eT
, k =
1-e-aT
![]() a
a
e, W =
M T ,
![]() a
a
получаем отображение
кольца
xn+1 = xn + W + k sin xn + brn ,
rn+1 = brn + k sin xn .
Параметр W отвечает за постоянное «вращение» переменной в отсутствии импульсов, параметр b характеризует диссипацию, а k – амплитуду внешних импульсов.
В случае сильной диссипации
a ® ¥
и тогда
b ® 0 . В этом случае первое
уравнение
отображения кольца редуцируется к синус-отображению окружно- сти:
xn+1 = xn + W + k sin
xn .
В случае отсутствия диссипации
a = 0
и b = 1. Таким образом, в консерва-
тивном случае отображение кольца приводится к
xn+1 = xn + W + k sin xn + rn ,
rn+1 = r + k sin xn .
16.
Получите отображение для
подталкиваемого ротатора в случае отсут- ствия постоянного вращающегося момента
– диссипативную и консервативную версии стандартного отображения.
Решение 16. В этом случае удобно выбрать запись первого уравнения, в
которой использовано значение переменной
кольца соответствующим образом, получаем:
rn+1.
Переписывая отображение
xn+1 = xn + W + rn+1, rn+1 = br + k sin xn .
В случае отсутствия постоянного вращающегося момента
xn+1 = xn + rn+1, rn+1 = br + k sin xn .
W = 0 , и тогда
Это
диссипативная версия стандартного
отображения. Консервативное стан- дартное отображение имеет вид:
xn+1 = xn + rn+1, rn+1 = r + k sin
xn .
Его еще называют отображением Чирикова-Тейлора.
17. Систему из задачи 15
иногда приводят к виду отображения Заславско-
го
![]() x = x + W +
x = x + W +
n+1 n 2p
K (1- e-Г
![]() G
G
) sin(2pxn ) +
1- e-Г
![]() G
G
yn ,
yn+1 = e-Г ( yn + e
sin 2pxn ).
Найдите выражения для параметров отображения Заславского. Миними- зируйте число параметров в отображении Заславского, и покажите, что оно приводится к отображению кольца.
Решение 17. Используем полученное в 15 размерное отображение
xn+1 =
xn + (yn
+
e sin xn
)1-e-aT
![]() a
a
+ M T ,
![]() a
a
yn+1 = (yn + e
sin xn )e-aT .
Если выполнить замену переменных и параметров
x ® 2px,
y ® 2py , G = gT , K = eT , W = MT ,
![]()
![]()
![]()
T 2p a
то оно приводится к отображению кольца. Отображение Заславского содержит четыре параметра, т.е. является «переопределенным» по сравнению с отобра- жением кольца.
18.
Рассмотрите неавтономный генератор
пилообразных колебаний5,
для которого момент запуска каждого очередного импульса управляется сигналом,
промодулированным по гармоническому закону U (t) = U0 + Um sin wt
около не-
которого среднего значения
U0 , рис.9. Получите дискретное отображение,
дающее зависимость момента начала (n+1)-го импульса
tn+1
от момента начала
n-го импульса tn
и покажите, что оно совпадает с синус-отображением окруж-
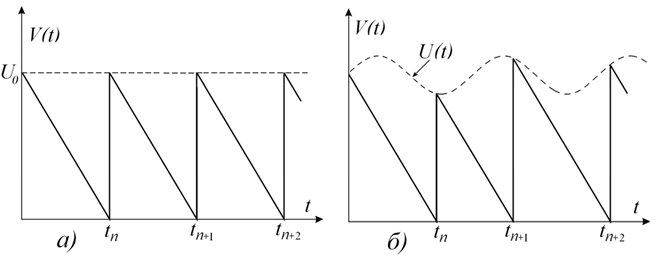
ности. Длительность импульсов в автономном режиме равна Т.
Рис.9.
Сигнал
автономного (а) и неавтономного (б) генератора пилообразных колебаний.
Решение 18. Для рассматриваемого генератора в автономном режиме в
диапазоне
tn < t < tn+1
выходной сигнал
V (t)
убывает от значения U 0
до нуля
по линейному закону:
V (t) =
U0
- U0 (t - t ) .
![]() T n
T n
После этого напряжение скачком увеличивается до величины
U0 , и про-
цесс повторяется. Колебания в этом случае будут периодическими во времени с периодом T.
Теперь введем внешнее воздействие, изменяющее верхний порог по гар- моническому закону: U (t) = U 0 + Um sin wt . В этом случае «стартовое» значение напряжения равно U (tn ) , и напряжение от времени в пределах одного импульса зависит от времени в соответствии с соотношением
![]()
5 Простейший
вариант физической модели такого генератора может быть реализован при помощи
неоновой лампы.
V (t) =
U (tn
) - U 0 (t - t
![]() T n
T n
) = U0
+ Um
sin wtn
- U 0 (t - t ) .
![]() T n
T n
![]() Нетрудно получить соотношение, связывающее моменты времени в которые
напряжение обращается в нуль:
Нетрудно получить соотношение, связывающее моменты времени в которые
напряжение обращается в нуль:
tn+1 и
tn ,
U0 + Um
sin wtn
- U0 (t T
n+1
- tn
) = 0 .
Разрешая это соотношение относительно tn+1 , получим:
tn+1
= tn
+ T (1+ Um sin wt ) .
n![]()
U0
Это и есть искомое отображение. Его удобно записать в безразмерном ви-
де, переходя к безразмерной переменной
qn = wtn :
qn+1 = qn + W + k sin qn .
В такой форме его
называют синус-отображением окружности.
Оно со-
держит два параметра. Один из них
W = wT
= 2pw/ w0 , где
w0 = 2p / T
– частота
собственных колебаний генератора. Поэтому параметр W можно интерпрети- ровать как расстройку по частоте внешнего сигнала и собственных колебаний
системы. Второй параметр
k = wTU m /U 0
представляет собой безразмерную
амплитуду внешнего воздействия.
Отметим, что из нашего рассмотрения можно получить общий вид ото- бражения окружности
где
f (q)
qn+1 = qn + W + k × f (qn ),
– 2p-периодическая функция. В рамках изложенной физической ин-
терпретации она задается законом модуляции внешнего сигнала. Она не обяза- тельно является гладкой, а может представлять собой импульсы прямоуголь- ной, треугольной или другой формы.
19. Пусть
имеется автоколебательная система, установившемуся режиму которой на фазовой
плоскости отвечает движение по предельному циклу в виде окружности радиуса
R, рис.10. В отсутствии внешнего воздействия за время t
точка поворачивается на угол
q = wt . Пусть на такую систему через определен-
ные моменты времени T действуют внешние импульсы, которые приводят к из- менению ординаты точки на постоянную величину – амплитуду импульса B. Такая модель была предложена канадским биофизиком Гласом для моделиро- вания биофизических систем. Получите одномерное отображение для перемен-
ной
qn . К кому типу оно относится? Для простоты положим частоту вращения
w = 1.
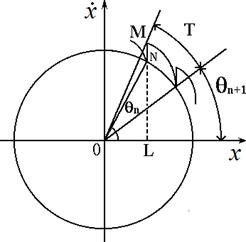
Рис.10. Иллюстрация
построения отображения для системы с предельным циклом под им- пульсным
воздействием.
Решение 19. Пусть изображающая точка непосредственно перед n-ым внешним импульсом находится в точке N и характеризуется углом qn , рис.10. В результате действия импульса изображающая точка на фазовой плоскости
«поднимается» вверх на величину В, и попадает в точку М. Затем наступает пе- риод автономной эволюции в течение времени Т, а изображающая точка успе- вает вернуться на предельный цикл. Теперь она характеризуется углом qn+1. Как видно из рис.10
tg(q
n+1
+ T ) = MN + NL .
![]() OL
OL
В свою очередь OL
= R cos qn , NL = R sin qn , MN=B. Поэтому
tg(q
n+1
+ T ) = B + R sin qn .
![]() 2R cosq
2R cosq
Разрешая это соотношение относительно бражение
n
qn+1 , получаем одномерное ото-
qn+1
= arctg(sin qn + C ) - T .
![]() cosq
cosq
Здесь С
= B / R
n
– нормированная амплитуда воздействия.
Это и есть отображение Гласа. Оно представляет собой вариант отобра- жения окружности.
20.
Получите отображение, описывающее
разгон релятивистской частицы в циклическом резонансном ускорителе заряженных
частиц — циклотроне. Частица вращается в однородном магнитном поле B с
циклотронной частотой
wc = qB0 / m
(q и m — заряд и масса частицы), периодически проходя через ус-
коряющий промежуток (зазор), к которому приложено высокочастотное напря-
жение
V (t) = V0 sin wt , рис.11. Если частота изменения ускоряющего напряже-
ния w близка к циклотронной частоте, частица будет каждый раз попадать в ускоряющую фазу, увеличивая свою энергию. Что будет в нерелятивистском случае?
Указание. Используйте релятивистское выражение для энергии частицы и постройте отображение для релятивистского масс-фактора и момента времени пролета зазора ускорителя.
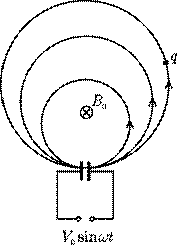
Рис.11. Разгон заряженной частицы в циклотроне.
Решение 20. Будем рассматривать динамику частицы в дискретные момен- ты времени, когда она проходит через ускоряющий промежуток. Считая этот промежуток достаточно узким, предполагаем, что частица проходит через него практически мгновенно (по сравнению с периодом высокочастотного напряже-
ния
T = 2p / w), так что изменением напряжения за это время можно пренеб-
речь. Поскольку речь идет о релятивистской частице, необходимым моментом является учет релятивистской зависимости массы от скорости.
![]() Энергия частицы после n-ого
прохода через ускоряющий промежуток рав-
Энергия частицы после n-ого
прохода через ускоряющий промежуток рав-
на En = mnc2 = gnm0c2 , где
m0 – масса покоя частицы,
gn = 1/
– реля-
тивистский масс-фактор. Закон сохранения энергии при прохождении зазора запишется следующим образом:
gn+1m0c2 = gnm0c2 + qV0 sin wtn ,
где tn
– время n-ого попадания в зазор. Следующее попадание в зазор, очевид-
но, произойдет в момент времени
tn+1
= tn
+ 2p
![]() wc (gn+1 )
wc (gn+1 )
= tn
+ 2pm0 gn+1 .
![]() qB0
qB0
Объединяя полученные уравнения и вводя обозначение для фазы частицы
qn = wtn
, приходим к двумерному отображению
qn+1 = qn + Dgn+1,
gn+1 = gn + k sin qn .
Здесь
k = qV0 / m0c2 , D = 2pw/
w0 ,
w0 = qB0 / m0 .
Нетрудно видеть, что мы полу-
чили стандартное отображение (отображение Чирикова-Тейлора), если ввести
переменную
Gn = Dgn :
qn+1 = qn + Gn+1,
Gn+1 = Gn + (kD) sin qn .
Если бы не релятивистская зависимость циклотронной частоты от энергии,
первое уравнение имело вид
qn+1 = qn + D , так что при совпадении частот w и
w0 частица после каждого оборота попадала бы в одну и ту же фазу поля и ус-
корялась неограниченно. В релятивистском случае с ростом энергии резонанс- ное условие нарушается.
21.
Получите двумерное отображение для
диссипативного осциллятора с импульсным возбуждением, амплитуда которого
зависит по гармоническому закону от координаты
x:
¥
0
&x& + 2ax& + w2 x = С sin x ×åd(t - nT ).
-¥
Отдельно рассмотрите консервативный случай (отображение-паутина) и приведите отображение к безразмерному виду.
Решение 21. Переменные выбираем аналогично задаче 14, так что
xn и vn
– координата и скорость осциллятора перед n-ым импульсом. Тогда после им-
пульса координата не изменится, а скорость станет равна
vn + C sin xn . Подстав-
ляя эти величины в качестве начальных значений в решение задачи 2, получаем координату и скорость осциллятора перед следующим импульсом:
xn+1
= e-aT (coswT + a sinwT
![]() w
w
) × xn
+ e-aT
1 sin wT × (v
![]() w n
w n
+
С sin xn ),
vn+1 = -e
-aT
a2 + w2
![]() w
w
sin wT × xn + e
-aT
(cos wT - a sin wT ) × (v + С sin x ).
![]() w n n
w n n
В консервативном случае, когда a = 0 , получаем:
xn+1
= cosw0T × xn +
1 w![]()
0
sin w0T ×
(vn
+
С sin xn ),
vn+1 = -w0 sin w0T × xn + cos w0T × (vn + С sin xn ).
Отнормируем теперь скорость и амплитуду воздействия на величину соб- ственной частоты осциллятора w0 . Тогда в безразмерном виде получаем:
xn+1 = cosd× xn + sin d × (vn + С sin xn ),
vn+1 = - sin d× xn + cosd×(vn + С sin xn ).
Безразмерный параметр
d = w0T
характеризует соотношение собственной
частоты осциллятора
w0
и частоты сигнала T / 2p.
Полученное отображение называют отображение-паутина. Название свя- зано
с тем, что в фазовом пространстве можно наблюдать ажурные структуры,
напоминающие паутину. При этом выделяют частные случаи тех или иных ре-
занасов, управляемых параметром a. Например, при a =
p
xn+1 = -xn ,
vn+1 = -vn - С sin xn ,
и т.д. Соответственно, в диссипативном случае имеем диссипативную версию отображения-паутины.
От потоков к отображениям: метод медленно меняющихся амплитуд
22.
С помощью метода медленно меняющихся амплитуд получите ото- бражение для
диссипативного осциллятора с кубической нелинейностью (ос- циллятор Дуффинга) с импульсным возбуждением:
¥
&x& + ax& + x + bx3
= С ×åd(t - nT ).
-¥
Здесь нормировка выбрана так, что собственная частота
w0 = 1. Покажите,
что оно может быть приведено к отображению Икеды. В случае сильной дис- сипации получите соответствующее приближенное одномерное отображение.
Комментарий. В работе Икеды с соавторами была рассмотрена оптическая система в виде кольцевого резонатора, частично заполненного средой с фазовой нелинейностью, рис.12. Резонатор возбуждается лучом лазера через одно полу- прозрачное зеркало, а выходной сигнал снимается через другое. При некоторых
n![]()
![]()
условиях такая система
может быть приближенно описана с помощью
отобра-
жения
zn+1
= A + Bzn
exp(i
z 2 ). Здесь z — комплексная амплитуда света, A —
параметр, пропорциональный сигналу лазера, B — параметр диссипации поля в среде.
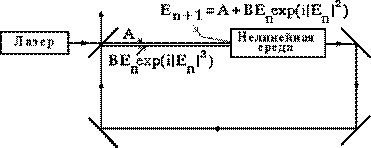
Рис.12.
Система
Икеды.
Решение 22. В рассматриваемом случае амплитуда внешних импульсов постоянна. Поэтому удобно следить за координатой и скоростью сразу после n-
для динамики на автономной стадии, рис.13.
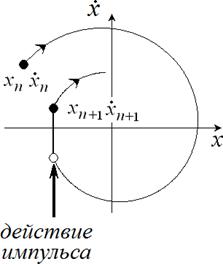
Рис.13. К
построению отображения для двумерной системы с импульсным возбуждением.
В промежутке между импульсами уравнение нелинейного осциллятора аналитически не решается. Можно, однако, воспользоваться приближенным решением с помощью метода медленно меняющихся амплитуд7. Для этого представим координату в виде:
x(t) = 1 (a(t)eit + a*(t)e-it ).
2
6 В задачах 14 и 15 использовались
переменные перед этим импульсом.
Отличия этих подхо- дов становятся существенными, если
амплитуда импульса зависит от координаты осцилля- тора.
7 Различные его
версии можно найти в литературе, мы рекомендуем [1,3,11].
Здесь
a(t)
– комплексная медленная амплитуда, звездочка отвечает ком-
плексному сопряжению. Поскольку мы ввели, фактически, две новых функции
a(t) и a* (t) , то на них можно наложить дополнительное условие, которое вы-
бирают в виде
a&(t)eit +
a&*(t)e-it
= 0 .
Дифференцируя выражение для координаты и используя дополнительное условие, получаем зависимость скорости от времени:
v(t) = x&(t) = 1 (a&(t)eit + a&*(t)e-it
)+ i (a(t)eit - a*(t)e-it
)= i (a(t)eit - a*(t)e-it
).
2 2 2
Она аналогична случаю постоянной амплитуды a, в чем и состоит удобство вы- бора дополнительного условия.
Теперь надо вычислить вторую производную от координаты:
&x&(t) = i (a&(t)eit - a&*(t)e-it
)- 1 (a(t)eit + a*(t)e-it
)= a&(t)eit + x(t).
2 2
Подставляем полученные соотношения в автономное уравнение Дуффинга. Затем оставляем в полученном уравнении только члены, отвечающие колебани-
ям на собственной частоте осциллятора и пропорциональные
eit
. Остальные на
фоне колебаний с основной частотой являются быстро осциллирующими, так что при усреднении за большой промежуток времени их вкладом можно пре- небречь.
Вклад кубической нелинейности определяется соотношением
x3(t) = 1 (aeit +
a*e-it )3 = 1 (a3e3it +
3a2a*(t)eit +
3a(a*)2
e-it
+ (a*)3e-3it )=
3 a2a*eit +
...
8 8 8
В результате приходим к укороченному уравнению для осциллятора Дуффинга:
a 3 2
![]()
![]()
![]()
![]() a& = - 2 a + 8 ib a a .
a& = - 2 a + 8 ib a a .
Введем действительную амплитуду
R(t)
и фазу
j(t)
с помощью соотно-
шения
a(t) = R(t)eij(t) . Тогда из комплексного укороченного уравнения после
разделения действительной и мнимой частей, получаем:
R& = -
a R ,
2
j = 3 bR2 .
&
8
Эти уравнения можно проинтегрировать, так что
R(t) = R
expæ- aT ö, j
![]()
= 3 b
![]()
2 1- e-gt + j
![]()
n ç 2 ÷
(t)
8 Rn g n ,
è ø
где Rn
и jn - начальные амплитуда и фаза сразу после n -го импульса.
Из исходных соотношений нетрудно получить, что
x(t) = R(t)
cos[t + j(t)] ,
v(t) = -R(t)sin[t + j(t)].
Теперь необходимо учесть действие импульса, так что
xn+1 = R(T
) cos[T + j(T )],
vn+1 = -R(T ) sin[T + j(T )] + C .
![]() Используя решения для амплитуды и фазы
Используя решения для амплитуды и фазы
R(t),
j(t) , получаем
-aT
3 2 1- e-aT
![]()
![]() xn+1 = Rne
xn+1 = Rne
2 cos(T +
8 bRn a + jn ),
-aT
3 2 1- e-eT
![]()
![]()
![]() vn+1 = -Rne
vn+1 = -Rne
2 sin(T +
8 bRn a +
jn ) + C.
Далее удобно использовать комплексное представление, вводя новую пе- ременную z:
z = (ix
+
v)
3 1- e-aT
b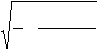
.
8 a
Используя, что
xn = Rn cos jn ,
vn = -Rn sin jn , так что
(ixn + vn ) =
= iRn exp(-ijn ) , получаем искомое отображение:
n+1 n n![]()
![]()
z = A + Bz exp(i( z 2 + T )) .
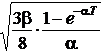 Параметры А, В определяются
через параметры исходной системы сле- дующим образом:
Параметры А, В определяются
через параметры исходной системы сле- дующим образом:
A = C
, B =
e-aT / 2 .
Это отображение Икеды. В рассматриваемом случае его параметры име- ют следующий смысл: A – безразмерная амплитуда сигнала, а B – параметр дис- сипации.
Если диссипация сильная и
B <<
1
(сильное сжатие на аттрактор), то ото-
бражение Икеды можно привести к одномерному. Для этого представим пере- менную z следующим образом:
z
= A(1 + B~z )
.
Подставим это выражение в левую и правую части отображения и разре-
шим его относительно переменной
~zn+1 :
~z = (1+
B~z
) exp[i(j + l Re ~z
+ 1 lB ~z 2
)] .
n+1 n
n 2 n
![]()
![]() Здесь введены новые параметры
Здесь введены новые параметры
l = 2 A2B ,
j
= A2 +
T .
Учтем малость В и оставив только слагаемые первого порядка малости. То-
гда для действительной части xn =
Re ~zn
следует одномерное отображение
xn+1 = cos(lxn + j) ,
которое заменой x=lx+j приводится к более удобному виду – «отображению косинуса»
xn+1 = lcos xn + j .
Заметим, что переход к одномерному отображению привел к уменьшению числа существенных параметров с трех до двух.
23.
С помощью метода медленно
меняющихся амплитуд получите двумер- ное отображение, описывающее осциллятор
Ван дер Поля с импульсным воз- буждением:
¥
&x& - (l
- x2 )x& + x = С ×åd(t -
nT ).
-¥
Покажите, что если импульсы «редкие», то полученное отображение реду- цируется к одномерному отображению Гласа для фазы изображающей точки.
Указание. Удобно строить отображение для комплексной переменной
z = x + iv .
Решение 23. Решение задачи аналогично предыдущей. Отличие состоит в
нелинейном члене
x&x2 , для которого получаем:
![]()
![]()
![]()
![]()
![]()
![]() x2
x& = 1 [a2e2it + 2 a 2 + (a*)2
e-2it ](iwaeit - iwa*e-it ) = 1 iw a 2 aeit
+ ...
x2
x& = 1 [a2e2it + 2 a 2 + (a*)2
e-2it ](iwaeit - iwa*e-it ) = 1 iw a 2 aeit
+ ...
8 8
Для автономной системы приходим к укороченному комплексному урав- нению
l 1 2
![]()
![]()
![]() a&
= 2 a - 8 a a,
a&
= 2 a - 8 a a,
и уравнению для действительных амплитуды и фазы
R& = l R - 1 R3,
j& = 0 .
2 8
Они интегрируются с соответствующими начальными условиями
Rn и
jn :
R(t) =
expæ lT ö , j(t) = j .
![]()
ç ÷ n
2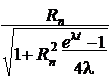
è ø
Действуя аналогично предыдущей задаче, получаем отображение для ко- ординаты и скорости
x = Rn cos(T + jn ) expæ lT ö,
![]()
n+1
ç ÷
+ 2 2
elT -1 è ø
1 R
n 4l
v = -
Rn sin(T + jn ) expæ lT ö + C.
![]()
n+1 ç ÷
2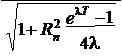
è ø
Вводя комплексную переменную
z = x + iv , находим
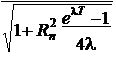 z = 1
z = 1
expæ lT - iT - ij ö + iC.
![]()
n+1
ç n ÷
2
è ø
Начальные амплитуда и фаза связаны с координатой и скоростью соотно-
шениями xn = Rn cosjn , vn = -Rn sin jn , так что zn = Rn exp(- ijn ). Тогда полу-
чаем искомое отображение:
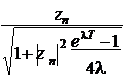 z = expæ lT -
iT ö + iС .
z = expæ lT -
iT ö + iС .
![]()
n+1 ç ÷
2
è ø
Это двумерное отображение, описывающее динамику автоколебательной системы с внешним импульсным воздействием.
Пусть импульсы являются «редкими». Тогда в промежутке между ними изображающая точка успевает вернуться к предельному циклу автономной системы. С физической точки зрения теперь можно следить только за фазой ко- лебаний, вычисляя ее значения непосредственно перед соответствующим им- пульсом. Проведем формальное рассмотрение, реализующее описанное поведе- ние.
Пусть lТ>>1 (период внешнего воздействия большой по сравнению с ха- рактерным временам релаксации). Из полученных выражений для координаты
и скорости при
e-lT ® 0
получаем:
xn+1 = 2
l cos(T + jn ) ,
vn+1 = -2
l sin(T + jn ) + С .
![]()
![]()
![]() Это решение отвечает выходу изображающей точки на автономную орбиту
Это решение отвечает выходу изображающей точки на автономную орбиту
радиуса
R0 = 2
с некоторой новой фазой. Для нее и необходимо построить
отображение
jn+1 =
f (jn ) .
что
Из xn+1 + ivn+1 = Rn+1 exp(-
ijn+1 )
и предыдущих соотношений, очевидно,
tgj
= - vn+1
= sin(T + jn ) - A ,
![]()
n+1
![]()
xn+1
cos(T + jn )
![]() где A = C
где A = C
имеет смысл нормированной амплитуды внешнего воздействия.
Удобно ввести новую фазу
qn = jn + T . Физически – это фаза изображающей
точке перед следующим импульсом. Тогда
tg(q
n+1
- T ) = sin qn - A ,
![]() cos q
cos q
n
откуда получаем искомое одномерное отображение:
qn+1
= arctg(sin qn - A) + T .
![]() cosq
cosq
n
Оно представляет собой отображение Гласа (с точностью до несуществен- ных знаков), полученное выше из чисто «геометрических» соображений в зада- че 19.
24.
С помощью метода медленно
меняющихся амплитуд получите двумер- ное отображение, описывающее осциллятор Ван
дер Поля-Дуффинга с им- пульсным возбуждением:
¥
&x& - (l
- x2
)x& + x +
bx3 =
С ×åd(t - nT ).
-¥
В случае «редких» импульсов получите
соответствующее отображение для фазы и обсудите, когда оно представляет собой
синус-отображение окружно- сти.
Решение 24. Решение задачи аналогично предыдущей, при этом необхо- димо использовать комбинированную нелинейность, отвечающую осциллято- рам Ван дер Поля и Дуффинга. В результате получаем следующее комплексное укороченное уравнение:
l 1 2 3 2
![]()
![]()
![]()
![]()
![]() a& = 2 a - 8 a
a& = 2 a - 8 a
a + ib a a.
![]() 8
8
Уравнение для действительных амплитуды и фазы:
R& = l R - 1 R3, j& = 3 bR2 .
2 8 8
Можно видеть, что в рассматриваемом случае динамика фазы зависит от амплитуды, что определяет неизохронность системы, т.е. зависимость периода автономных колебаний от амплитуды.
Уравнение для амплитуды не изменилось, и можно использовать решение предыдущей задачи. Подставляя его в уравнение для фазы, и интегрируя с на- чальным условием jn , получаем
j(t) = jn +
2
3 R![]()
![]()
bln n (elt 2 4l
-1) +1 .
![]() Действуя аналогично предыдущей задаче, получаем:
Действуя аналогично предыдущей задаче, получаем:
z æ lT
3 z 2 ö
2 2 è ø
![]()
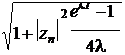
![]()
![]()
![]()
zn+1 =
n expç - iT -
i bln n (elT -1) +1
÷ + iC.
ç 4l ÷
Это и есть искомое двумерное отображение. Можно видеть, что введение дополнительной нелинейности по типу осциллятора Дуффинга привело к отли- чию в законе динамики фазы.
Получим теперь отображение в случае «редких» импульсов. Считая
![]() lT >> 1, и учитывая это как в амплитудном множителе, так и в фазе, получаем
lT >> 1, и учитывая это как в амплитудном множителе, так и в фазе, получаем
xn+1 = 2
l cos(T + jn +
![]() 3
3
3 blT +
![]() 2
2
![]() 3
3
3 R2
![]()
![]()
![]() bln n ) = 2 2 4l
bln n ) = 2 2 4l
![]()
![]() R2
R2
l cosqn ,
![]() vn+1 = -2
vn+1 = -2
l sin(T + jn +
blT +
![]() 2
2
bln n ) + C = -2 2 4l
l sin qn + C.
![]() Здесь по аналогии с предыдущей задачей введена новая фаза
Здесь по аналогии с предыдущей задачей введена новая фаза
qn = jn + T +
3 blT +
![]() 2
2
3 R2
![]()
![]()
![]() bln n , 2 4l
bln n , 2 4l
отвечающая моменту времени перед следующим импульсом.
Как и в предыдущем случае
tgj
n+1
= - vn+1
![]()
![]() xn+1
xn+1
= sin qn - A , cosqn
![]() где A = C
где A = C
. Поэтому осталось выразить
jn+1
через новую фазу
qn+1
. При этом
![]()
![]() нужно вычислить
нужно вычислить
R
2
n+1
2
= x
n+1
2
+ v
n+1
= (2
l cosqn
)2 + (2
l sin qn
+ A)2 = 4l(1- 2 Asin qn
+ A2 ).
Окончательно
q
= arctg(sin qn - A)
+ W +
3 bln(1- 2 Asin q
![]()
![]()
+ A2 ) ,
n+1
cosqn 2
n![]()
где W = T(1 + 3 bl)
2
имеет смысл нормированного периода воздействия.
Мы получили некоторую разновидность отображения окружности, которая
при нулевой неизохронности b = 0
приводится к отображению Гласа.
Пусть амплитуда сигнала A мала. Тогда, разлагая в ряды по A, получаем:
qn+1 = qn - A cosqn + W - 3bAsin qn .
При этом использовали формулу
arctg (tgj + e) » j + ecosj.
Возмущение отображения поворота
qn+1 = qn + W
будет сильным, если
bA~1. Оно может быть обеспечено даже при малых амплитудах воздействия A,
если неизохронность b достаточно велика, и тогда:
qn+1 = qn + W - 3bAsin qn .
Мы получили стандартное синус-отображение окружности. Основные приближения, которые при этом были сделаны: возвращаемость траектории на предельный цикл, малые амплитуды воздействия и большая неизохронность.
25.
Покажите, что если амплитуда
внешних импульсов мала, так что дина- мика осциллятора из предыдущей задачи
происходит вблизи автономного пре- дельного цикла, то в случае большой
неизохронности система может быть опи- сана отображением кольца для фазы
колебаний и отклонения действительной амплитуды от положения равновесия.
Решение 25. Отличие от двух предыдущих задач состоит в том, что мы те- перь учтем динамику изображающей точки в небольшой окрестности предель-
ного цикла. Далее удобнее использовать значения амплитуды и фазы
Rn и jn
перед импульсом. Поэтому сначала необходимо учесть действие импульса. Он приводит к значениям координаты и скорости
x =Rn cosjn , v = -Rn sin jn + C,
Значения амплитуды и фазы после импульса
R(0) и
j(0)
можно найти из
![]() чисто «геометрических» соотношений, используемых в предыдущих задачах:
чисто «геометрических» соотношений, используемых в предыдущих задачах:
tgj(0) = Rn sin
jn - C ,
![]()
R(0) =
(R cosj )2 + (R sin j
- C)2 .
Rn cosjn
n n n n
![]()
![]() Учтем также, что движение происходит вблизи автономного предельного
Учтем также, что движение происходит вблизи автономного предельного
цикла
R0 = 2
, так что
R = 2
+
r , где r – малая величина. Тогда из приве-
денных соотношений при малой амплитуде импульсов C можно получить в первом порядке по С:
C![]()
j(0) = jn -
cosjn ,
r(0)
= rn
- C sin jn .
(Также использовали формулу
arctg(tgj + e) » j + ecosj.)
Уравнения для амплитуды и фазы в промежутке между импульсами имеют
вид:
R& = l R - 1 R3, j& = 3 bR2 .
2 8 8
![]() Из амплитудного уравнения, подставляя получаем:
Из амплитудного уравнения, подставляя получаем:
R = 2
+ r , с учетом малости
r
r& = -lr.
Начальным условием для него является
r(0) . Это уравнение легко интег-
рируется и приводит к выражению:
r(t) = r(0)e-lt .
![]()
![]() Подставим найденный закон изменения амплитуды зовое уравнение и, считая
добавку малой, получаем:
Подставим найденный закон изменения амплитуды зовое уравнение и, считая
добавку малой, получаем:
R = 2
+ r(0)e-lt
в фа-
![]()
![]()
![]() j& = 3
bR2 = 3 bl + 3 b
j& = 3
bR2 = 3 bl + 3 b
lr(0)e-lt .
8 2 2
Интегрируя его с начальным условием фазы, так что через время T:
j(0), получаем закон изменения
jn+1
= j(T ) = j(0) + 3 blT +
![]() 2
2
(1- e-lT )r(0).
![]() Сюда надо подставить найденные значения начальных амплитуды и фазы
Сюда надо подставить найденные значения начальных амплитуды и фазы
r(0)
и j(0)
с учетом rn+1 = r(0)e-aT . Тогда
![]()
![]() C 3
C 3
3b(1- e-lT )
jn+1 = jn -
cosjn + 2 blT +
2 le-lT
rn+1,
![]() rn+1 = (rn - C sin jn )e-lT .
rn+1 = (rn - C sin jn )e-lT .
Далее нужно принять приближение большой неизохронности, так что
![]() j = j +
3 blT +
j = j +
3 blT +
n+1 n 2
3b(1- e-lT )
![]()
rn+1,
rn+1
= rne-lT - Ce-lT sin jn .
Убирая в первом уравнении множитель перед нормируя величину С, получаем отображение кольца
jn+1 = jn + W +
rn+1,
rn+1 = br -
k sin xn ,
rn+1
перенормировкой, и
где W =
3 blT
, b = e
![]() 2
2
-lT ,
3b(1- e-lT )C k = .
![]() Нетрудно сформулировать физические требования к системе, чтобы полу-
чалось это отображение: наличие предельного цикла, экспоненциально быстрое
приближение траектории к предельному циклу и сильная неизохронность сис- темы.
В этом плане отображение кольца является достаточно универсальным.
Нетрудно сформулировать физические требования к системе, чтобы полу-
чалось это отображение: наличие предельного цикла, экспоненциально быстрое
приближение траектории к предельному циклу и сильная неизохронность сис- темы.
В этом плане отображение кольца является достаточно универсальным.
отображению окружности
jn+1 = jn + W - 3bC sin jn , что совпадает с результа-
![]() том предыдущей задачи (с учетом C
= 2 l A ).
том предыдущей задачи (с учетом C
= 2 l A ).
26.
Рассмотрите систему типа
осциллятора Ван дер Поля с импульсным возбуждением
где
¥
&x& - (e
- mx2
)x& + x =
F (x) åd(t -
nT ),
n=-¥
F (x) = 1 - lx2 . Получите соответствующее отображение при
T = p (4k + 1) .
![]() 2
2
Покажите, что оно сочетает свойства автоколебательной системы как с устой- чивым, так и с неустойчивым предельными циклами, а также свойства систем с удвоениями периода (по типу отображения Эно).
Решение 26. Используем значения координаты и скорости
xn , vn
перед n-
ым импульсом. Действуя аналогично предыдущим задачам, с помощью метода медленно меняющихся амплитуд нетрудно получить отображение
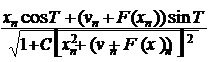 xn+1 = B ,
xn+1 = B ,
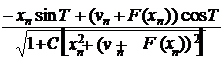 v =
B ,
v =
B ,
где
n+1
![]() B = exp(eT / 2) , C = mT (exp eT - 1) 4eT .
B = exp(eT / 2) , C = mT (exp eT - 1) 4eT .
Положим для простоты
T = p (4k + 1)
![]() 2
2
и используем конкретный вид функ-
1+ C x2 + (1- lx2 + v )2![]()
xn+1 = B [ ],
vn+1
= -B
n n n
![]() xn .
xn .
Она характеризуется «внутренними» параметрами e и m и «внешним» па- раметром l, определяющим вид функции F(x). Параметр ε отвечает за величину линейной диссипации (отрицательного трения при ε>0), параметр m характери-
8 Такое отображение предложено Кузнецовым С.П.
![]() зует нелинейную диссипацию в автономной системе. Соответственно, при
по- ложительных значениях этих параметров автономная система демонстрирует
устойчивый предельный цикл, размер которого при небольшом превышении
зует нелинейную диссипацию в автономной системе. Соответственно, при
по- ложительных значениях этих параметров автономная система демонстрирует
устойчивый предельный цикл, размер которого при небольшом превышении
над порогом
бифуркации Андронова-Хопфа можно оценить как r »
. Если
эти параметры отрицательны, то в системе имеет место неустойчивый предель- ный цикл.
Если нелинейная диссипация отсутствует (m=0 в дифференциальной сис- теме, С=0 в отображении), то отображение (2.10) переходит в диссипативное отображение Эно
n
xn+1 = B(1- lx2 + yn ),
yn+1 = -Bxn .
Если при этом отсутствует и линейная диссипация (ε=0, B=1), то оно пере- ходит в консервативное отображение Эно
n
xn+1 = 1 - lx2 + yn ,
yn+1 = -xn .
Отметим, что требование возможности такого предельного перехода и оп-
ределило выбор функции
F (x) = 1- lx2 . Таким образом, отображение сочетает
свойства автоколебательной системы и системы с удвоениями периода.
27.
Покажите, что одномерная потоковая
система всегда градиентна. Ка- кую
физическую интерпретацию можно дать в этом случае? Какие результаты теории
катастроф по этой причине можно перенести в теорию бифуркаций?
Решение 27. Уравнение одномерной динамической системы в общем слу-
чае имеет вид
x& =
f (x) . Вводя функцию U (x) = -ò f (x)dx,
¶U (x)
получаем:
![]() x&
+ ¶x = 0.
x&
+ ¶x = 0.
Таким образом, одномерная динамическая система является градиентной, т.е. описывается с помощью потенциала U (x) . В физическом плане это уравне- ние отвечает частице, движущейся в потенциальном поле в среде с очень силь-
ной вязкостью.
Состояния равновесия такой системы, используя терминологию теории ка-
тастроф, отвечает
критическим точкам функции U (x) .
При этом минимумы
отвечают устойчивым равновесиям, а максимумы – неустойчивым. Соответст- венно, классификация катастроф и бифуркаций в одномерной системе совпада- ет. Приведем таблицу соответствия терминов.
|
теория катастроф |
теория бифуркаций |
|
складка |
седло-узел |
|
сборка |
трехкратное равновесие |
|
ласточкин хвост |
четырехкратное равновесие |
И так далее.
28.
Найдите закон изменения
во времени переменной
x(t) для бифуркаций
седло–узел, заданной уравнением
x& = l - x2 , и вилка, заданной уравнением
x& = lx - x3 ,
при
l> 0
и l< 0 . Обсудите асимптотическое поведение этих зави-
симостей при увеличении времени.
Решение 28. Бифуркация седло-узел в одномерной системе описывается соотношением
x& = l - x2 .
Это уравнение можно проинтегрировать:
ò ò
dx = dt .
l - x2
Интеграл является табличным, так что при l > 0
íï
x(t) = ìï
î
l × th(
![]()
![]()
![]()
![]() l × cth(
l × cth(
l(t - с)), x <
![]()
![]()
![]()
![]()
![]()
![]() l(t - с)),
x > l.
l(t - с)),
x > l.
Здесь c – постоянная интегрирования, определяемая начальной точкой и за- дающая семейство траекторий. В частотности, для первого соотношения при x(0) = 0 будет с=0.
![]() Используя асимптотические выражения для гиперболических функций,
Используя асимптотические выражения для гиперболических функций,
получаем, что при
t ® ¥
выполняется соотношение
x(t) ®
l. Это решение
![]() отвечает устойчивому равновесию системы. В свою очередь, значение -
отвечает устойчивому равновесию системы. В свою очередь, значение -
бифуркации седло-узел, в которой сливаются устойчивое и неустойчивое рав- новесия.
Рекомендуем самостоятельно построить семейство зависимостей x(t) , а
также обсудить случай
l< 0 .
Для бифуркации вилка уравнение имеет вид: можно проинтегрировать при l> 0 :
ò ò
dx = dt .
lx - x3
x& = lx - x3 . Это уравнение
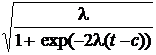 Интеграл является табличным, так что после интегрирования получаем
Интеграл является табличным, так что после интегрирования получаем
±
ì
ï
í![]()
![]()
![]()
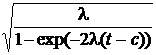
x(t) = ï
, x < l,
ï![]()
![]()
![]()
ï ± , x > l.
î
Здесь c – постоянная интегрирования.
Из полученных соотношений следует, что при
![]()
![]() t ® ¥ , в зависимости от
t ® ¥ , в зависимости от
начальных условий, решение приходит или в точку
+
, или в точку
- ×
Это устойчивые равновесия системы. От точки
x = 0
траектории «отталкивают-
ся», и она является неустойчивым равновесием. Все три равновесия сосущест-
вуют при
l > 0
и сливаются в точке бифуркации l = 0 .
Рекомендуем построить графики семейства зависимостей
x(t)
и обсудить
случай
l< 0 .
29.
Изобразите бифуркационные диаграммы для бифуркаций седло–узел,
транскритической бифуркации и вилки.
![]()
9 Траектории приходят
в него, если в уравнении обратить время.
Решение 29. Бифуркационные диаграммы, дающие зависимость координат состояний равновесия от параметра l, приведены в верхнем ряду на рис.14. Сплошной линией показаны устойчивые равновесия, пунктирной – неустойчи- вые. Стрелкой отмечено бифуркационное значение параметра.
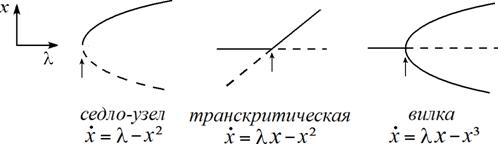
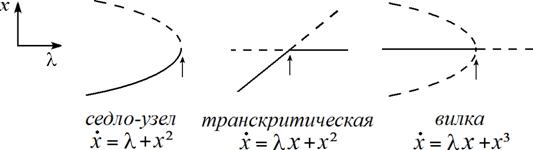
Рис.14 Бифуркационные
диаграммы для суперкритических бифуркаций одномерных пото- ков (вверху) и
субкритических (внизу).
30.
Изобразите бифуркационные диаграммы для обратных (субкритиче-
ских) форм этих бифуркаций.
Решение 30. Иллюстрации в предыдущей задачи отвечали прямым (супер- критическим) формам основных бифуркаций одномерных потоков. Для обрат- ных (субкритических) форм бифуркационные диаграммы и уравнения приведе- ны на рис.14 в нижнем ряду.
31. Для бифуркации
трехкратное равновесие (сборка)
x& + x3 + ax2 + bx = 0 ,
изобразите линии седло-узловых бифуркаций на плоскости параметров (b, a) .
Укажите вид потенциала в разных точках плоскости в соответствии с интерпре- тацией задачи 27.
Решение 31. Состояния равновесия системы ищем из уравнения
x3 + ax2 + bx = 0 . Поскольку это кубическое уравнение, то их число может быть
рано трем10 или одному. Седло-узловая бифуркация отвечает слиянию этих равновесий, так что ее условие получаем, дифференцируя полученное соотно-
шение по x:
3x2 + 2ax + b = 0 . Решая эти уравнения совместно, находим линии
седло-узловых бифуркаций:
![]() 3
3
b = ±2æ- a ö 2
.
![]()
ç ÷
3
è ø
На плоскости параметров
(b, a)
они образуют полукубическое острие в
точке сборки b = a = 0 , имеющей коразмерность два, рис.15.
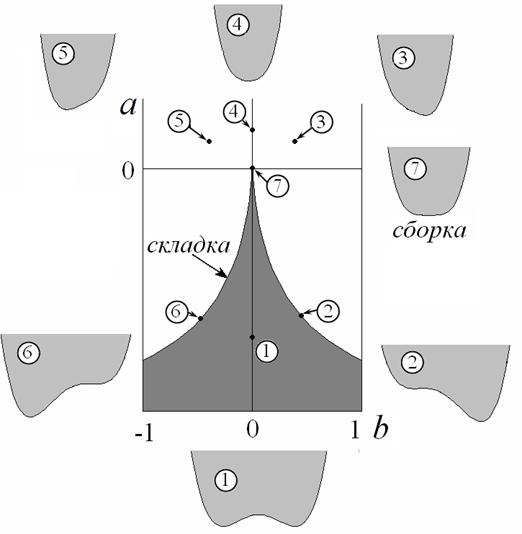
Рис.15.
Трансформации
потенциала для бифуркации трехкратное равновесие (сборка).
О характере равновесий в системе удобно следить с помощью потенциаль-
ной функции, которая в рассматриваемом случае
U (x) =
x3 +
![]()
3
ax2
![]() 2
2
+ bx . На
рис.15 показаны конфигурации потенциала в характерных точках плоскости параметров, позволяющие определить число состояний равновесия и их устой- чивость. Внутри области, показанной серым цветом, система имеет два устой- чивых и одно неустойчивое равновесия.
32.
Обсудите связь с катастрофой сборка
бифуркаций вилки и вилки в слу- чае снятия вырождения. Используйте трехмерный
рисунок многообразия ката- строфы сборки и бифуркационные диаграммы, дающиеся
его сечениями.
Решение 32. Пусть система описывается потенциалом, характерным для катастрофы сборка
U (x) =
x3 +
![]()
3
ax2
![]() 2
2
+ bx.
Уравнение состояний равновесия такой системы
x3
+ ax2
+ bx = 0
задает в
трехмерном пространстве (b,a,x) поверхность, показанную на рис.16. Ее назы- вают многообразием катастрофы сборка. Проекция этой поверхности на плос- кость параметров (b,a) дает двухпараметрическую картину, соответствующую рис.15 из предыдущей задачи.
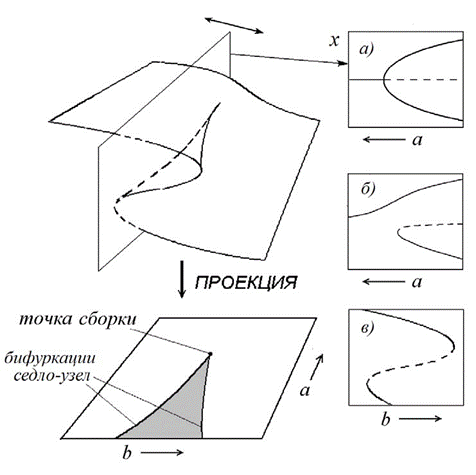
Рис.16. Связь
многообразия катастрофы сборка и основных бифуркаций одномерных пото- ков: а)
вилка, б) «вилка со снятым вырождением», в) седло-узел.
На рис.16а показано сечение поверхности, проходящее через точку сборки и отвечающее бифуркации вилка. Если немного «пошевелить» сечение, изменяя параметр b, как показано двусторонней стрелкой, то перейдем к ситуации «вил- ка со снятым вырождением» (рис.16б). Если построить перпендикулярную к этому сечению плоскость, то можно будет увидеть бифуркационные диаграммы двух объединенных седло-узловых бифуркаций (рис.16в). На общем рисунке они видны, как «торцевая» часть поверхности многообразия катастрофы.
33.
Выпишите в общем виде уравнения,
задающие двумерную потоковую динамическую систему, уравнения для определения
состояний равновесия этой системы и матрицу возмущений. Укажите возможные
варианты расположения собственных чисел этой матрицы на комплексной плоскости и
постройте соот- ветствующие типичные (грубые) фазовые портреты состояний равновесия.
Решение 33. Двумерная система в общем случае задается уравнениями
x& =
f (x, y),
Состояния равновесия ния переменных:
(x0 , y0 )
y& = g(x, y).
ищем, приравнивая нулю скорости измене-
f (x0 , y0 ) = 0,
g(x0 , y0 ) = 0.
Динамика малых возмущений переменных в окрестности состояния равно- весия будет определяться матрицей возмущений
ˆ æ fx¢(x0 , y0 ) f y¢(x0 , y0 ) ö
M = ç g¢ (x , y ) g¢ (x , y ) ÷ .
è x 0 0 y 0 0 ø
Здесь соответствующие частные производные вычислены в точке равновесия.
Для определения характера равновесия необходимо найти собственные значения g этой матрицы. Поскольку она имеет порядок «два на два», то урав- нение для поиска собственных чисел является квадратным уравнением с дейст- вительными коэффициентами. Поэтому имеется два собственных числа, кото- рые могут быть либо действительными, либо комплексно-сопряженными. Кон- фигурация собственных чисел на комплексной плоскости и типичные фазовые портреты состояний равновесия с их названиями даны на рис.17.
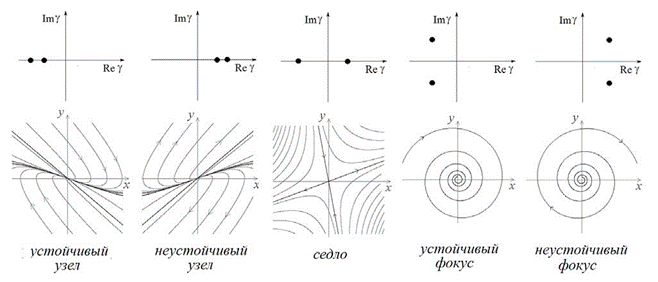
Рис.17. Положение
собственных чисел матрицы возмущений двумерного потока на ком- плексной
плоскости и типичные фазовые портреты состояний равновесия.
34.
С помощью матрицы возмущений проведите
анализ типов состояний равновесия двумерной динамической системы. Результат
представьте на плос- кости след S –
якобиан J этой матрицы и
проиллюстрируйте фазовыми портре- тами в тех или иных областях на плоскости параметров.
Решение 34. Пусть имеется двумерная потоковая система общего вида, ко- торой отвечает матрица возмущений Mˆ в точке равновесия. Как было отмечено при решении предыдущей задачи, уравнение для определения собственных чи-
сел или
g1, g2
является квадратным. Поэтому, очевидно, справедливо соотношение
(g - g1 )(g - g2 ) = 0,
g2-(g1 + g2
)g +
g1g2 = 0.
Входящие в это
уравнение коэффициенты определяют два инварианта
матрицы возмущений: ее след S и якобиан J:
S = g1 + g2
, J =
g1g2 .
Эти величины удобно использовать как параметры при исследовании ха- рактера равновесий. Собственные числа определяются через эти параметры с
помощью соотношения
g2-Sg + J = 0, так что
g1,2
= S ±
![]() 2
2
S 2
-
J .
4
Они будут действительными, если
J < S 2 / 4
и комплексными при
J > S 2 / 4 . При этом возможны пять вариантов, которым отвечает пять типов грубых состояний равновесия двумерных потоков.
1) 0 < J < S 2 / 4 , S < 0 . Оба собственных
числа действительные и отрица-
тельные. Равновесие является устойчивым узлом.
2)
0 < J < S 2
/ 4 , S > 0 . Оба собственных
числа действительные и положи-
тельные. Равновесие является неустойчивым узлом.
3) J <
0 . Оба собственных числа действительные, одно из них положи-
тельное, а одно – отрицательные. Равновесие является седлом.
4) J > S 2 / 4 , S <
0 . Собственные числа комплексные (комплексно-
сопряженные), причем
Reg < 0 . Равновесие является устойчивым фокусом.
5) J > S 2 / 4 , S >
0 . Собственные числа комплексные (комплексно-
сопряженные), причем
Reg > 0 . Равновесие
является неустойчивым фокусом.
Разбиение плоскости параметров след – якобиан на указанные области приведено на рис.18. Там же показаны характерные фазовые портреты соответ- ствующих равновесий11.
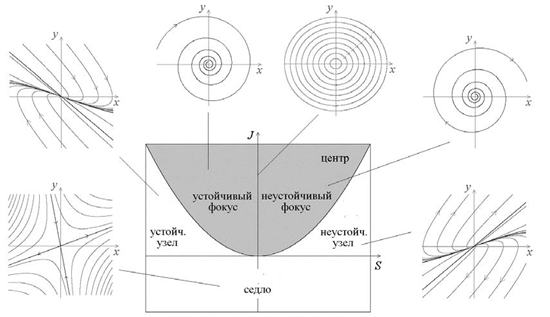
Рис.18. Различные типы неподвижных точек на плоскости
след S - якобиан J
матрицы
линеаризации.
Представленные результаты обладают свойством универсальности, т.е. не зависят от вида динамической системы. При анализе конкретной системы, та- ким образом, достаточно найти выражения для следа и якобиана матрицы воз- мущения для данного равновесия через параметры отображения, и далее ис- пользовать готовые результаты рис.18.
![]()
11 Отметим, что на линии S=0, J>0
реализуется вырожденная ситуация, когда состояние рав- новесие имеет тип центр. Эту ситуацию можно
интерпретировать как консервативный слу- чай.
35.
Изобразите положение собственных
чисел матрицы возмущений на комплексной плоскости, отвечающее бифуркациям седло-узел, Андронова- Хопфа и Богданова-Такенса.
Продемонстрируйте с помощью этих иллюстра- ций, что точка Богданова-Такенса
является общей для бифуркаций седло-узел и Андронова-Хопфа.
Решение 35. При вариации параметров, задающих двумерный поток, соб- ственные числа будут перемещаться по комплексной плоскости. При этом бу- дут возникать бифуркационные ситуации, отвечающие перестройке топологии фазового портрета. Используя картину расположения собственных чисел на комплексной плоскости на рис.18, нетрудно выявить основные типы возмож- ных бифуркаций. В результате получаем четыре основных негрубых ситуации, представленные на рис.19. В подписи к рисунку даны условия на собственные
числа
g1,2 , отвечающие каждой бифуркации.
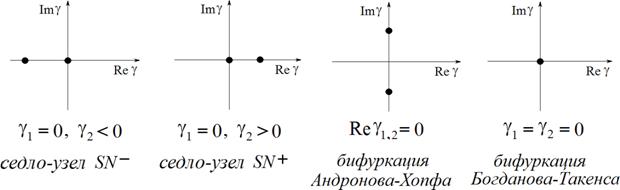
Рис.19. Конфигурация
собственных чисел матрицы возмущений двумерного потока на комплексной
плоскости, отвечающая типичным бифуркациям.
В первых двух случаях одно из собственных чисел проходит через ноль. Это условие отвечает седло-узловой бифуркации. Нетрудно видеть, что для дву- мерного потока возможны два варианта такой бифуркации. «Пошевелим» не-
много параметры. При этом в первом случае обозначенном
SN - , собственное
число может уходить немного вправо или влево от начала координат12. Тогда возникают седло или устойчивый узел. Поэтому в этом случае седло сливается
с устойчивым узлом. Во втором случае, обозначенным
SN + , седло сливается с
неустойчивым узлом. В этом отличие от одномерного потока, где наблюдается единственный вариант седло-узловой бифуркации.
В третьем случае пара комплексно сопряженных собственных чисел пере- секает мнимую ось. Это условие отвечает превращению устойчивого фокуса в
12 Верхний индекс у
обозначения SN отвечает знаку второго
собственного значения.
неустойчивый (или наоборот). Такая ситуация отвечает бифуркации Андронова- Хопфа, когда фокус теряет устойчивость и от него отделяется неустойчивый предельный цикл. Отметим, что возможна и обратная (субкритическая) бифур- кация Андронова-Хопфа, когда возникает неустойчивый предельный цикл
Фиксируем теперь параметр, отвечающий бифуркации Андронова-Хопфа. Если варьировать второй параметр, то собственные числа будут перемещаться вдоль мнимой оси, и при некотором значении этого параметра сливаются, что приводит к ситуации, показанной на четвертом рисунке. Это точка бифуркации Богданова-Такенса. Таким образом, точка Богданова-Такенса является конце- вой для бифуркации Андронова-Хопфа. Если фиксировать ситуацию, отвечаю- щую седло-узловой бифуркации, то при вариации дополнительного параметра второе собственное число будет перемещаться вдоль действительной оси, и также можно добиться ситуации слияния. Поэтому точка Богданова-Такенса является общей для бифуркации Андронова-Хопфа и седло-узел.
36.
Изобразите качественно фазовые
портреты, отвечающие бифуркации седло-узел двумерного потока.
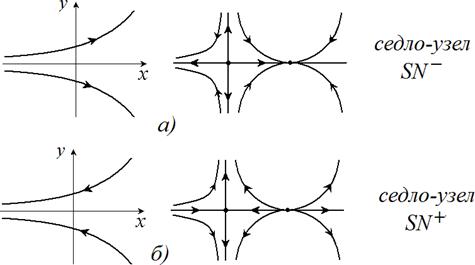
Решение 36. Фазовые
портреты показаны на рис.20. Для двумерного по- тока возможны два варианта
седло-узловой бифуркации. В первом случае ус- тойчивый узел сливается с седлом,
а во втором – неустойчивый.
Рис.20. Седло-узловые
бифуркации двумерного потока: а) слияние устойчивого узла и седла, б) слияние
неустойчивого узла и седла.
37.
Изобразите качественно фазовые
портреты, отвечающие бифуркации Андронова-Хопфа двумерного потока. Рассмотрите
случаи суперкритической и субкритической формы
бифуркации.
Решение 37. Фазовые портреты для бифуркации Андронова-Хопфа пока- заны на рис.21. При этом рис.21а отвечает прямой (суперкритичесокй), а
рис.21б – обратной (субкритической) форме. В первом случае при изменении управляющего параметра устойчивый фокус превращается в неустойчивый, и от него отделятся устойчивый предельный цикл. Во втором случае с ростом па- раметра неустойчивый предельный цикл «влипает» в устойчивый фокус, в ре- зультате чего возникает неустойчивый фокус. Используется обозначение, где нижний индекс «– » отвечает устойчивому фокусу, а «+» - неустойчивому13.
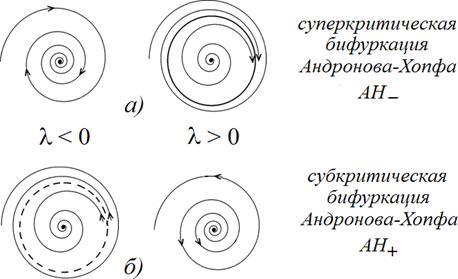
Рис.21.
Суперкритическая и субкритическая бифуркация Андронова-Хопфа на фазовой
плоскости.
38.
Найдите условия бифуркаций
седло-узел, Андронова-Хопфа и Богда- нова-Такенса, используя в качестве
параметров след и якобиан матрицы воз- мущений.
Решение 38. След и якобиан связаны с собственными числами соотноше-
ниями
S = g1 + g2 ,
J = g1g2.
Условием бифуркации седло-узел является обращение в ноль одного из
собственных чисел
g1,2 . Поскольку
J = g1g2 ,
то это означает обращение в ноль
якобиана матрицы возмущений.
Бифуркация Андронова-Хопфа отвечает превращению устойчивого фоку- са в неустойчивый. Это означает, что ее условием являются чисто мнимые соб-
ственные значения, т.е.
g1 = ia ,
g2 = -ia . Подставляя эти соотношения в
S = g1 + g2 ,
J = g1g2 ,
получаем:
S = 0, J
> 0.
Перечисленные бифуркации являются однопараметрическими, или, как го- ворят, бифуркациями коразмерности один. Если варьировать два параметра, то могут встретиться бифуркации коразмерности два. Так общая точка бифурка- ции седло-узел и Андронова-Хопфа отвечает бифуркации Богданова-Такенса.
Таким образом, можно прийти к следующим результатам:
·
бифуркация
седло-узел: J =
0,
·
бифуркация Андронова-Хопфа:
S = 0, J
> 0,
·
бифуркация (точка) Богданова-Такенса:
S = 0, J
= 0.
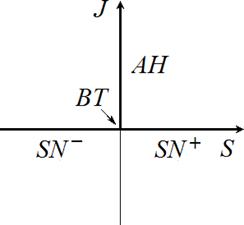
На плоскости след – якобиан эти бифуркации задают конфигурацию,
пока- занную на рис.22. Знаками «плюс» и «минус» обозначены две разновидности
седло-узловой бифуркации, когда сливаются устойчивый узел и седло, или не-
устойчивый узел и седло. Эта картина является универсальной для двумерных
потоков.
Рис.22. Линии
бифуркаций Андронова-Хопфа AH,
седло-узел SN и точка
Богданова-Такенса BT двумерного
потока на плоскости след – якобиан матрицы возмущений. Верхний индекс различает
два типа седло-узловых бифуркаций, отвечающих рис.20.
39. Рассмотрите
уравнение математического маятника с затуханием:
&x& + ax& + sin x = 0 .
Здесь нормировка выбрана так, что собственная частота осциллятора равна единице. Найдите состояния равновесия и определите их тип с помощью под- хода, изложенного в задаче 34.
Решение 39. Представим уравнение осциллятора в стандартном для дина- мической системы второго порядка виде:
x& = v,
v& = -av - sin x.
Состояния равновесия ищем, приравниваю нулю производные по времени, что дает
v0 = 0, sin x0 = 0.
Таким образом, система имеет два состояния равновесия (с учетом 2p-
периодичности), для которых
x0 = 0 и
x0 = p.
Матрица возмущений имеет вид:
ˆ æ 0 1 ö
ø
M = ç
è
- cos x0
- a÷.
Ее след ищем, складывая диагональные члены:
S = -a , а также вычисляем
якобиан
J = cos x0 .Таким образом, след всегда отрицательный. В свою очередь,
для равновесия
x0 = 0
якобиан
J = 1 и положительный. В соответствии с рис. 18
это отвечает устойчивому равновесию. Используя условие превращения узла в
фокус
J = S 2 / 4 , получаем, что равновесие будет фокусом при
a / 2 < 1 и узлом
при
a / 2 > 1.
Для равновесия
x0 = p
якобиан
J = -1 и отрицательный, так что эта точка
неустойчива и всегда является седлом.
Физически проведенный анализ достаточно понятен: нижнее положение равновесия маятника является устойчивым. При малом затухании оно является фокусом (периодическое затухание), а при большом – узлом (апериодическое затухание). Верхнее положение равновесия всегда является неустойчивым и отвечает седлу.
40.
Пусть маятник из предыдущей задачи
прикреплен к спиральной пру- жине с коэффициентом жесткости k, так
что
&x& + ax& + kx + sin x = 0 .
Маятник может совершать любое число полных оборотов вокруг точки прикрепления. Напишите уравнение для определения положений равновесия, дайте его графическое решение. Покажите, что число устойчивых равновесий уменьшается при увеличении жесткости пружины. Проведите физическое об- суждение полученных результатов. Найдите бифуркации в системе.
Решение 40. Запишем уравнения для определения состояний равновесия:
v0 = 0, kx0 + sin x0 = 0.
Физически это отвечает равенству нулю скорости и суммарного момента, создаваемого пружиной и силой тяжести. Полезно проанализировать это урав-
нение графически. Для этого на одном рисунке изображаем функции
y = sin x и
y = - kx . Точки их пересечения и определяют положения равновесия системы, как показано на рис.23.
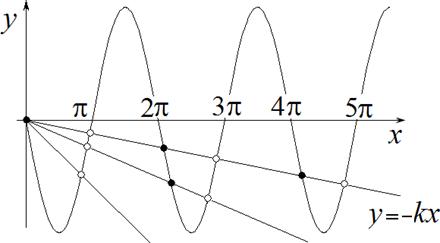
Рис.23. Графическое
определение состояний равновесия маятника с пружиной.
Из рисунка можно видеть, что число состояний равновесия зависит от же- сткости пружины k , и с ее уменьшением появляются все новые состояния рав- новесия, когда график прямой пересекает синусоиду во все более далеких точ- ках.
Проанализируем возможные решения с использованием физических пред- ставлений. Пусть параметр k стремится к нулю, т.е. пружина очень «мягкая» и почти не оказывает влияния на систему. Как видно из рисунка, решения в этом
случае стремятся к значениям угла 0, p,
2p,
3p ,
4p и т.д. Это положения рав-
новесия свободного маятника. При этом углам p, 3p , … отвечает неустойчивое равновесие, когда маятник вертикален, а груз находится в верхней точке. Углам
0, 2p, 4p… отвечает нижнее положение маятника, т.е. устойчивое равновесие.
На рис.23 устойчивые состояния равновесия отмечены жирными точками, а не- устойчивые – кружочками. Если пружины нет, то эти равновесия сводятся к двум вариантам: нулевой угол и угол, равный p. Остальные неотличимы от них. (Они соответствуют поворотам маятника вокруг точки подвеса на угол, крат-
ный
2p.) Однако наличие даже очень мягкой пружины снимает эту симметрию,
и делает состояния равновесия различающимися.
Будем теперь медленно увеличивать жесткость пружины, что отвечает на графике увеличению наклона прямой. Устойчивые и неустойчивые состояния равновесия будут попарно двигаться навстречу друг другу. При бифуркацион- ных значениях параметра они также попарно будут сливаться и исчезать. Реко- мендуем обсудить с физической точки зрения, почему моменты бифуркаций
близки к точкам
3 p,
![]() 2
2
5 p,
![]() 2
2
7 p…
![]() 2
2
Дадим теперь формальное решение задачи. Матрица возмущений
ˆ æ 0 1 ö
ø
M = ç
è
- k - cos x0
- a÷.
В точках равновесий ее след
S = -a , а якобиан
J = -k - cos x0 . Можно ви-
деть, что в системе возможна бифуркация седло-узел, когда выполняется усло-
вие
J = 0 , так что
k + cos x0 = 0 . Совместно с уравнением для поиска состояний
равновесия, это приводит к уравнению для бифуркационных значений:
k = -cos x0 , x0 = tgx0 .
Эти уравнения можно решить численно, например, методом Ньютона. Это дает последовательность бифуркаций:
k1 = 0.21723... ,
k2 = 0.12837...,
k3 = 0.09132…
41.
Проведите анализ состояний
равновесия и их бифуркаций для осцилля- тора Ван дер Поля
&x& - (l - x2 )x& + x = 0 .
Решение 41. Используем представление динамической системы в стан- дартной форме
x& =
v,
v& = (l - x2
)v - x.
ç ÷.
В данном случае состояние равновесия
тривиальное: ца возмущений в этой точке
v0 = 0, x0 = 0.
Матри-
Ее след
S = l , а якобиан
Mˆ = æ 0 1ö
l
è -1 ø
J = 1.
Таким образом, в системе возможна бифуркация Андронова-Хопфа при
значении параметра
l = 0 . Физически это понятно: при
l < 0
система пред-
ставляет собой диссипативный осциллятора, а при рицательным, и фокус становится неустойчивым.
l > 0
трение становится от-
Отметим также, что с ростом параметра l устойчивый фокус в начале ко-
ординат при узел.
l = 2
(находим из условия
J = S 2 / 4 ) превращается в устойчивый
42.
Запишите укороченные уравнения для
действительной амплитуды ос- циллятора Ван дер
Поля
&x& - (l - x2 )x& + x = 0 ,
С его помощью определите тип бифуркации, соответствующий бифурка- ции Андронова-Хопфа в исходной системе. Оцените размер возникающего пре-
дельного цикла и покажите, что при увеличении управляющего параметр l его размер растет по корневому закону. Получите закон, по которому изображаю- щая точка стремится к предельному циклу. Покажите, что характерное время выхода изображающей точки на предельный цикл уменьшается с ростом пара- метра l.
Решение 42. Для осциллятора Ван дер Поля укороченные уравнения по- лучены в задаче 23:
R& = l R - 1 R3
,
j& = 0 .
2 8
Нетрудно видеть, что амплитудное уравнение отвечает бифуркации вилка.
Действительно, при
l < 0
есть единственное устойчивое равновесие
R0 = 0 .
При
l > 0
состояние равновесие с нулевой амплитудой теряет устойчивость, и
от него отделяются два устойчивых равновесия
R0 = ±2
l . Однако, поскольку
![]()
![]() действительная амплитуда R определяет
радиус на фазовой плоскости, то физи-
действительная амплитуда R определяет
радиус на фазовой плоскости, то физи-
ческий смысл имеет только положительный корень
R0 = 2 .
Отсюда следуют такие выводы для исходной системы. При
l < 0
устой-
чивым является равновесие в начале координат. Оно отвечает отсутствию авто- колебаний в исходной системе.
![]() ем:
ем:
При
l > 0 , возвращаясь к исходным переменным (см. задачу 23), получа-
![]() x(t) = 2
x(t) = 2
l cosT ,
v(t) = -2
l sin T .
![]() Это решение отвечает
вращению по окружности радиуса 2 с единич-
Это решение отвечает
вращению по окружности радиуса 2 с единич-
ной частотой. Таким образом, в исходной системе Ван дер Поля в результате бифуркации Андронова-Хопфа возникает устойчивый предельный цикл, размер которого растет по корневому закону в зависимости от надкритичности.
Отметим, что в приближении медленных амплитуд колебания являются изохронными – их частота равна единице и не зависит от параметра и, соответ- ственно, от радиуса предельного цикла.
![]() Линеаризуем амплитудное уравнение в окрестности предельного цикла.
Линеаризуем амплитудное уравнение в окрестности предельного цикла.
Полагая
R = 2
+ r , для малой величины r получаем:
r& = -lr . Таким образом,
r(t) = r(0) exp(-lt) . Поэтому параметр l характеризует также скорость выхода изображающей точки на предельный цикл. Чем больше l, тем быстрее точка выходит на предельный цикл.
43. Для осциллятора Ван
дер Поля
&x& - (l - x2 )x& + x = 0 ,
постройте реализации и фазовые портреты для нескольких значений параметра
l. Сравните с результатами, полученными с помощью метода медленно ме- няющихся амплитуд.
Решение 43. Фазовые портреты осциллятора Ван дер Поля и вид реализа-
ций
x(t)
при увеличении параметра l показан на рис.24. Можно видеть, что в
системе действительно происходит бифуркация Андронова-Хопфа, и возникает предельный цикл.

Рис.24. Фазовые портреты
(слева) и временные реализации колебаний (справа) осциллятора
Ван дер Поля; l = 0.1 (а), l = 1.1 (б); l = 10 (в).
При
l = 0.1
форма предельного цикла близка к окружности, радиус кото-
![]() рой хорошо оценивается из метода медленно
меняющихся амплитуд, как 2
рой хорошо оценивается из метода медленно
меняющихся амплитуд, как 2
(см. предыдущую задачу). Можно видеть медленный характер установления стационарных колебаний и «локально» синусоидальный характер последних.
С ростом l размер предельного цикла растет. При l » 1 форма предельно-
го цикла заметно искажается, и возрастает скорость установления стационар- ных колебаний. Таким образом, заметно уменьшается время выхода траектории на предельный цикл.
При больших l колебания становятся релаксационными, и предельный цикл искажается очень сильно. Состояние равновесия в начале координат явля-
ется уже не фокусом, а неустойчивым узлом. При этом система теряет свойство изохронности: период колебаний растет, что хорошо видно из сравнения реали- заций на рис.24б и рис.24в.
44.
Получите уравнение по типу
осциллятора Ван дер Поля, отвечающее субкритической форме бифуркации Андронова-Хопфа.
Решение 44. Такое уравнение имеет вид:
&x& - (l + x2 )x& + x = 0 .
В этом случае при
l > 0
в системе имеется устойчивый фокус, что физиче-
ски отвечает отрицательному трению. При
l < 0
фокус становится устойчивым,
и от него отделяется неустойчивый предельный цикл. Этот факт можно обосно- вать, выписав уравнение для медленной амплитуды:
![]()
![]() R& = l R + 1 R3
,
R& = l R + 1 R3
,
2 8
которое отвечает субкритичской форме бифуркации вилка.
Однако проще всего это сделать, заметив, что приведенное уравнение по- лучается из исходного уравнения Ван дер Поля обращением времени, т.е. заме-
ной
t ® -t
и изменением знака управляющего парамтера. При этом устойчивые
равновесия заменяются на неустойчивые и наоборот. Соответственно, устойчи- вый предельный цикл превращается в неустойчивый.
45.
Найдите порог бифуркации
Андронова–Хопфа в уравнениях химиче- ского автоколебательного осциллятора – брюсселятора:
x& = a - (b +1)x + x2 y, y& = bx - x2 y.
Решение 45. Приравнивая
нулю производные по времени, находим со- стояние равновесия брюсселятора:
x = a, y = b .
![]()
0 0 a
Вычисляя соответствующие частные производные от функций переменных x и y, задающих динамическую систему, находим матрицу возмущений в этой точке:
0 0 ˆ
æ- b -1
+ 2x
y
M = ç
2 ö
x 0 ø
0 ÷ .
è b - 2x0 y0
- x2 ÷
Подставляя сюда координаты равновесий, получаем:
ˆ
æb -1
è
M = ç- b
2 ö
. a 2 ÷
÷
- a ø
След этой матрицы
S = b - a2 -1. Условие бифуркации Андронова-Хопфа – об-
ращение в нуль следа матрицы Вычислим также якобиан
S = 0 , что приводит к равенству b - a2 -1 = 0 .
J = a2 . Таким образом, якобиан всегда положи-
тельный, и второе условие бифуркации Андронова-Хопфа выполнено. Отме-
тим, что параметр a управляет степенью сжатия в фазовом пространстве.
46.
Найдите пороговое значение
параметра n, отвечающее бифуркации Ан-
дронова-Хопфа для системы, описывающей колебания в гликолизе
x& = 1- xyn,
y& = a(xyn - y).
Решение 46. Сначала ищем положения равновесия системы: тем находим матрицу возмущения в этой точке:
x = y = 1. За-
ø
ˆ æ-1
- n ö
a
M = ç
è
a(n -1) ÷ .
Вычисляя ее след
S = an - a
-1
и якобиан
J = a, получаем условие би-
фуркации Андронова-Хопфа:
an = a + 1 и
a > 0 .
47.
Одна из разновидностей моделей
«хищник–жертва» может быть пред- ставлена в виде
Если положить
x& = a(x)x - xy,
y& = xy - my.
a = const , то мы получим классическую модель Вольтера14.
Покажите, что если функция
a(x) , характеризующая мальтузианский рост
«жертвы», монотонно убывает, то для случая сосуществования двух видов не- возможна бифуркация Андронова–Хопфа, а если она имеет квадратичный мак- симум, то такая бифуркация возможна. Обсудите устойчивость равновесий в
системе с функцией
a(x) , типа показанной на рис.25, рассмотрев ситуации:
а) жертвы вымирают, б) хищники и жертвы сосуществуют, в) хищники выми- рают. Обсудите возможные бифуркации в системе с ростом параметра m. Ука- жите решения, имеющие биологический смысл.
Решение 47. Уравнения для состояний равновесия имеют вид:
(a(x0 )
- y0 )x0 = 0, ( x0 - m) y0 = 0.
![]()
14
Подробнее см. Ю.М.Свирежев. Нелинейные диссипативные структуры и катастрофы в
экологии, 1983. М.: Наука, 368 с.
Рис.25. К модели «хищник-жертва».
Если жертвы вымирают и
x0 = 0 , то из второго уравнения автоматически
получаем и
y0 = 0 . Таки образом, эта точка отвечает вымиранию обоих видов.
Исследуем ее устойчивость. Вычисляем матрицу возмущений
ˆ æa¢(x0 ) x +
a(x0 ) - y0
- x0 ö
M = ç
è y0
x - m ÷ .
ø 0
ˆ æa(0)
0 ö
ø
Для тривиальной неподвижной точки
M = ç
è
0 - m÷. Таким образом, след
матрицы S = (a(0) - m), а якобиан
J = -ma(0) . Поскольку
a(0) > 0
(рис.26), то
якобиан отрицательный, и тривиальное равновесие является седлом. Таким об- разом, в данной системе оно всегда неустойчиво.
Исследуем теперь случай, когда хищники и жертвы сосуществуют. Тогда
для состояния равновесия получаем:
мущения в этой точке:
x0 = m,
y0 = a(m) . Находим матрицу воз-
ø
ˆ æma¢(m)
- mö
M = ç
è
a(m) 0 ÷ .
След матрицы возмущений
S = ma¢(m) , а якобиан
J = ma(m) .
Если функция
a(m) монотонно убывает, то
a¢(m) ¹ 0 , и бифуркация Анд-
ронова-Хопфа невозможна. Если же функция
a(m)
имеет квадратичный макси-
1
мум, то след может обратиться в ноль, и
бифуркация Андронова-Хопфа стано- вится возможной.
Бифуркационное значение m1
находим из уравнения
a¢(m ) = 0 . В окрест-
ности этой точки всегда
a(m) > 0
(рис.26), и поэтому якобиан
J = ma(m)
поло-
жительный, так что и второе условие бифуркации Андронова-Хопфа выполне- но.
Рис.26. К определению
бифуркационных параметров модели «хищник-жертва».
Будем теперь постепенно увеличивать параметр m. При
m < m1
след мат-
рицы возмущений отрицательный, и поэтому имеем неустойчивый фокус, ок-
руженный устойчивым предельным циклом. При
m = m1
предельный цикл сли-
вается с состоянием равновесия (бифуркация Андронова-Хопфа), и возникает устойчивый фокус, который затем переходит в устойчивый узел. Далее с рос-
том m величина
a(m)
начинает уменьшаться. При
m = m2 , когда
a(m2 ) = 0
(рис.26), якобиан обращается в ноль. Нетрудно видеть, что это отвечает ситуа- ции, когда исследуемое состояние равновесия отвечает вымиранию хищни- ков: y0 = a(m2 ) = 0 . При этом, однако, состояние равновесия не исчезает, а пре- вращается в седло, поскольку якобиан становится отрицательным. Значение пе- ременной y тоже становится отрицательным, и такое решение не является био- логически мотивированным.
В системе возможно еще одно равновесие, когда
y0 = 0
(хищники выми-
рают), а
x0 ¹ 0
(жертвы выживают). В этом случае
y0 = 0 , а x0
в неявной фор-
ме задается уравнением
a(x0 ) = 0 , где x0
– установившаяся численность жертв.
Матрица возмущений в этом случае
ˆ
æ x0a¢(x0 )
- x0 ö
ø 0
M = ç
è 0
x - m÷ .
Ее след
S = x0a¢(x0 ) + x0 - m , а якобиан
J = x0a¢(x0 ) (x0 - m) . Поскольку в
точке
x = x0
функция всегда убывающая (см. рис.25), то
a¢(x0 ) < 0 . Поэтому
при больших значениях параметра m якобиан отрицательный, и равновесие яв-
ляется седлом. При условии
m = x0 = m2
якобиан обращается в ноль. Это точка
бифуркации: седло сливается с равновесием второго типа. При этом, однако, равновесие не исчезает, а из седла превращается в узел. Поскольку след S = m2a¢(m2 ) отрицательный, то этот узел устойчивый.
Таким образом, в системе, благодаря ее симметрии, при прохождении че-
рез значение
m = m2
происходит транскритическая бифуркация: устойчивый
узел сливается с седлом, после чего узел превращается в седло, и наоборот. От- метим, однако, что возникшее седло не имеет биологического смысла.
48.
Для осциллятора Богданова
&x& - (m
- x)x& + a -
x2
= 0,
введите потенциальную функцию U (x) . Найдите состояния равновесия и обсу- дите их устойчивость с физической точки зрения. Затем выполните формаль- ный анализ и получите условия бифуркаций седло-узел, Андронова-Хопфа и
Богданова-Такенса. Укажите линии и точки бифуркаций на плоскости парамет-
ров и постройте характерные фазовые портреты. Обсудите возможность нело- кальной бифуркации предельного цикла.
Решение 48.
Осциллятор
Богданова – это каноническая модель, демонст- рирующая бифуркацию Богданова-Такенса. Осциллятор
Богданова можно представить в форме
![]() &x& - (m
- x)x& +
&x& - (m
- x)x& +
dU (x) dx
= 0 ,
где потенциальная функция
x3
U (x)
задана кубическим полиномом:
U (x) =
ax -
. Этот потенциал при
![]() 3
3
a < 0
не имеет экстремумов, а при
a > 0
ха-
рактеризуется наличием максимума и минимума, рис.27.
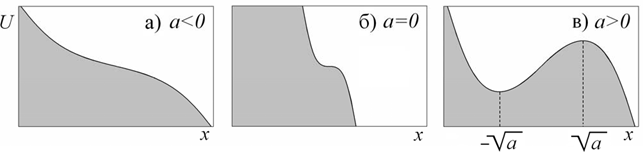
Рис.27. Потенциальная
функция осциллятора Богданова в зависимости от параметра a.
Таким образом, в системе возможны устойчивое и неустойчивое равнове-
2
0![]()
сия x0 , которым отвечает
равенство нулю действующей силы f (x) = a - x = 0 .
Поэтому получаем
x0 = ±
. Из вида потенциальной функции очевидно, что
верхний знак соответствует неустойчивой точке, а нижний – устойчивой. Таким образом, параметр a управляет взаимным положением экстремумов и отвечает
за бифуркацию слияния и исчезновения состояний равновесия, которая имеет
место при условии
a = 0 .
Член
(m -
x)x&
в уравнении осциллятора может характеризовать как поло-
![]() жительную, так и отрицательную диссипацию. При этом параметр m отвечает за
возможность возникновения автоколебаний, а значит – за бифуркацию Андро-
нова-Хопфа. Ее условие легко найти из физических соображений. Действитель- но,
диссипация меняет знак с положительного на отрицательный при условии
жительную, так и отрицательную диссипацию. При этом параметр m отвечает за
возможность возникновения автоколебаний, а значит – за бифуркацию Андро-
нова-Хопфа. Ее условие легко найти из физических соображений. Действитель- но,
диссипация меняет знак с положительного на отрицательный при условии
m - x0 = 0 , где для устойчивой неподвижной точки
x0 = -
. Следовательно,
![]() бифуркация Андронова-Хопфа имеет место при m =
- .
бифуркация Андронова-Хопфа имеет место при m =
- .
Таким образом, осциллятор имеет все «предпосылки» для реализации точ- ки бифуркации Богданова-Такенса при вариации двух существенных парамет- ров, один из которых, a, отвечает за бифуркацию седло-узел, а второй, m, за би- фуркацию Андронова-Хопфа.
Получим условия бифуркаций формальным образом. Для этого переписы- ваем уравнение осциллятора в стандартной форме
x& = v,
v& =
(m
- x)v - a +
x2
,
и находим матрицу возмущений в точках равновесий:
æ 0 1 ö
M = ç
è± 2
÷.
![]()
![]() m
m а ø
m
m а ø
![]()
![]() Теперь находим след и якобиан матрицы возмущений
Теперь находим след и якобиан матрицы возмущений
S = m
+ m ,
J =
m2 .
![]() Нетрудно видеть, что верхний знак («правое» равновесие) отвечает отри-
цательному якобиану, так что эта точка всегда является седлом. Нижний знак
отвечает точке, которая может быть устойчивой. Приравнивая нулю след, полу-
Нетрудно видеть, что верхний знак («правое» равновесие) отвечает отри-
цательному якобиану, так что эта точка всегда является седлом. Нижний знак
отвечает точке, которая может быть устойчивой. Приравнивая нулю след, полу-
чаем условие бифуркации Андронова-Хопфа
m = -
, а приравнивая нулю
якобиан, находим условие седло-узловой бифуркации
a = 0 . Точка Богданова-
Такенса отвечает одновременному выполнению этих условий, так что m = a = 0 . Естественно, мы получили те же результаты, что и из физических соображений. На рис.28 показаны линии основных бифуркаций коразмерности один в окрестности точки бифуркации Богданова-Такенса и фазовые портреты систе-
![]()
15 Представлена
наиболее интересная четверть плоскости параметров. Рекомендуем само- стоятельно изобразить фазовые портреты в остальных
случаях.
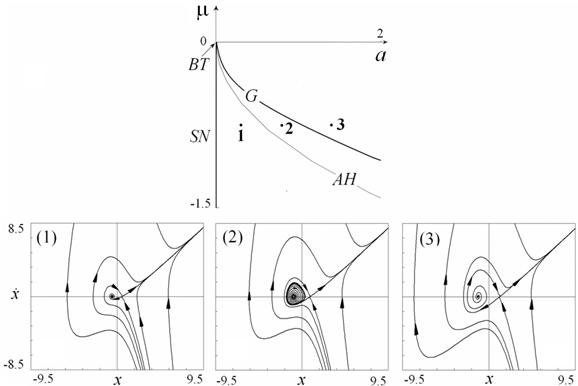
Такенса находится в начале координат. Можно видеть характерные
метаморфо- зы фазового портрета системы. В точке 1 в системе есть устойчивый
фокус и седло. При переходе через линию бифуркации Андронова-Хопфа фокус теряет
устойчивость и от него отделяется устойчивый предельный цикл, который уве-
личивается в размере, точка 2.
Рис. 28. Бифуркационные
линии осциллятора Богданова в окрестности точки Богданова- Такенса BT на плоскости параметров и фазовые
портреты в характерных точках. AH –
линия бифуркации Андронова-Хопфа, SN –
линия бифуркации седло-узел, G –
линия влипания пре- дельного цикла в петлю сепаратрисы.
Затем наблюдается еще одна бифуркация – бифуркация влипания предель- ного цикла в петлю сепаратрисы седла, в результате которой предельный цикл исчезает, точка 3. Появление такой бифуркации также понятно из качественных соображений. Действительно, в системе имеется седло, так что при увеличении предельного цикла в размере он сближается с седлом и, в конечном итоге, дол- жен «столкнуться» с ним. Линия влипания предельного цикла в петлю сепарат- рисы G не может быть найдена аналитически: ее приходится искать численно. Эта линия также подходит к точке Богданова-Такенса.
Заметим, что влипание предельного цикла в петлю сепаратрисы относится к нелокальным бифуркациям, для которых перестройка фазового портрета про- исходит в некоторой неисчезающее малой области фазового пространства.
49. Найдите условия
основных бифуркаций состояний равновесия осцил-
лятора с произвольной диссипативной функцией g(x) под действием произ-
вольной силы
f (x):
&x& - g(x)x& +
f (x) = 0 .
Решение 49. Представим уравнения в стандартной для динамических сис- тем второго порядка форме:
x& = y,
y& = g(x) y -
f (x).
Приравнивая нулю левые части, находим состояния равновесия
y0 = 0, f (x0 )
= 0.
Матрица линеаризации имеет вид:
æ 0 1 ö
= .
ç
M ç
f ¢(x )
÷
÷
g(x )
Ее след и якобиан
S = g(x0 ),
è 0 0 ø
J = f ¢(x0 ) .
Таким образом, получаем для бифуркаций коразмерности один.
·
Бифуркация седло-узел. Этой бифуркации отвечает
равенство нулю яко-
биана
J = 0 :
f (x0 ) = 0 ,
f ¢(x0 ) = 0 .
·
Бифуркация Андронова-Хопфа. Для этой бифуркации след
S = 0
при до-
полнительном условии
J > 0 , так что
f (x0 ) = 0 , g(x0 ) = 0 , f ¢(x0 )
> 0 .
Для бифуркаций коразмерности два получаем следующие условия.
·
Бифуркация
Богданова-Такенса. Эта бифуркация представляет собой об- щую точку бифуркаций село-узел
и Андронова-Хопфа, так что одновре-
менно
S = 0 ,
J = 0 . Тогда получаем
f (x0 ) = 0 , g(x0 ) = 0 , f ¢(x0 )
= 0 .
·
Бифуркация
трехкратное равновесие (точка сборки). Эта
бифуркация отвечает слиянию двух ветвей седло-узловой бифуркации, так что для нее
f (x0 )
= 0 ,
f ¢(x0 ) = 0 ,
f ¢¢(x0 ) = 0 .
В принципе, могут наблюдаться и бифуркации более высокой коразмерно- сти, например, четырехкратное равновесие («ласточкин хвост») и т.д.
Заметим, что осциллятор Богданова принадлежит к рассматриваемому
классу, и для него
g(x) = m - x и
f (x) = a - x2
.
50.
Для автогенератора с жестким возбуждением, описываемого урав- нением
&x& - (l + mx2-x4 )x& + x = 0 ,
получите укороченное уравнение. С его помощью обсудите бифуркации в сис- теме, включая бифуркации предельных циклов. Результат представьте на плос-
кости параметров
(m, l) . Параметр l , отвечающий за трение, и параметр m, от-
вечающий за нелинейное насыщение, могут быть как отрицательными, так и положительными.
Решение 50. Прежде всего, получим укороченное уравнение для автогене- ратора с жестким возбуждением. По сравнению с задачей 23 надо учесть влия-
![]()
![]() ние члена
ние члена
x4 x& . Действуя аналогично задаче 23, получаем
![]() x4
x& =
x4
x& =
i [a4e4it + 4 a 2
a2e2it + 6a2 (a*)2 + 4a(a*)3e-2it + (a*)4
e-4it ]´ 32
![]()
![]() ´(aeit - a*e-it ) = a 4 aeit + ...
´(aeit - a*e-it ) = a 4 aeit + ...
![]()
![]() Тогда приходим к следующему укороченному уравнению
Тогда приходим к следующему укороченному уравнению
l
![]() a& = 2 a +
a& = 2 a +
a 2 a -
a 4 a .
![]()
![]() Состояния равновесия укороченного уравнения ищем, приравнивая ско-
рость изменения амплитуды нулю. Одно из них располагается в начале коорди- нат.
Для нетривиального равновесия получаем:
Состояния равновесия укороченного уравнения ищем, приравнивая ско-
рость изменения амплитуды нулю. Одно из них располагается в начале коорди- нат.
Для нетривиального равновесия получаем:
x2 - 2mx - 8l = 0 ,
где x =
a 2 . Решаем это уравнение:
![]()
![]()
![]() x1,2 =
m ± .
x1,2 =
m ± .
При этом важно учесть, что должно быть
x = a 2 > 0 . Тогда в зависимости
![]()
![]() от комбинации знаков получаем следующие результаты:
от комбинации знаков получаем следующие результаты:
![]() l > 0 , x =
m + m2 + 8l
,
l > 0 , x =
m + m2 + 8l
,
![]() l < 0, m < 0 , решения нет,
l < 0, m < 0 , решения нет,
l < 0, m > 0 ,
x1,2 =
m ± .
Поскольку амплитуда a задает предельные циклы в исходной системе, то
заключаем, что при
l > 0
будет единственный предельный цикл, а при
l < 0, m < 0
предельных циклов нет. При
l < 0, m > 0
реализуется два предель-
ных цикла, если только
m2 > -8l . Рекомендуем самостоятельно показать, что
орбита меньшего радиуса (знак минус) отвечает неустойчивому режиму, а ор- бита большего (знак плюс) – устойчивому.
С помощью решения задачи 40 и 42 с учетом выбранных знаков в уравне-
нии заключаем, что линия
l = 0
отвечает бифуркации Андронова-Хопфа. При
этом она будет суперкритической (прямой)
AH -
при
m < 0
и субкритической
(обратной)
AH +
при m > 0 .
Суммарное устройство плоскости параметров
(m, l)
показана на рис.29.
Линия
l = 0
отвечает бифуркации Андронова-Хопфа. При
l = m = 0
располо-
Andronov-Hopf
жена точка коразмерности два, в которой меняется характер
бифуркации Анд- ронова-Хопфа. Такую точку называют вырожденной бифуркацией Андронова-
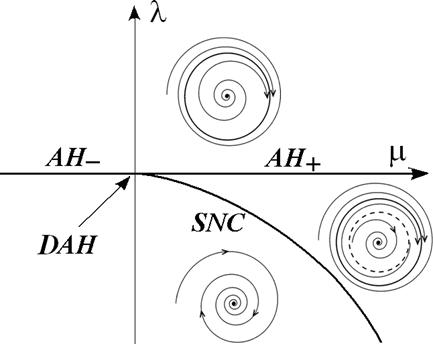
Рис.29.
Окрестность
точки вырожденной бифуркации Андронова-Хопфа DAH. На рисунке
показаны:
AH- – суперкритическая
бифуркация Андронова-Хопфа,
AH +
– субкритическая
бифуркация Андронова-Хопфа, SNC – линия слияния устойчивого и неустойчивого предель- ных
циклов. Пунктиром показан неустойчивый предельный цикл.
Если на плоскости параметров рис.29 обойти точку DAH по часовой стрел- ке, начиная с третьей четверти, то можно наблюдать такие метаморфозы фазо- вого портрета. Сначала имеется единственное состояние равновесия – устойчи-
перкритическая бифуркация Андронова-Хопфа, равновесие становится неус-
![]()
16 Иногда говорят об
обобщенной бифуркации Андронова-Хопфа.
тойчивым и от него отделяется устойчивый предельный цикл. При пересечении
линии
AH +
происходит субкритическая бифуркация Андронова-Хопфа, так что
равновесие превращается в устойчивый фокус и от него отделяется неустойчи-
вый предельный цикл. В области между линиями
AH+ и SNC в системе сосуще-
ствуют устойчивый и неустойчивый предельные циклы, а также устойчивое равновесие в начале координат. При уменьшении параметра λ предельные цик-
лы сближаются и на
линии SNC
m2 = -8l
сливаются и исчезают. Такую бифур-
кацию можно назвать седло-узловой бифуркацией предельных циклов.
51. Рассмотрите автоколебательный осциллятор с потенциалом
&x& - (l
- x2 )x& + x3 + ax + b = 0 ,
управляемым двумя параметрами a и b. Выпишите потенциальную функцию. Найдите условия локальных бифуркаций коразмерности один и два, и укажите
их на плоскости параметров (b, a) . Постройте примеры фазовых портретов и
укажите на возможность нелокальных бифуркаций.
Решение 51.Уравнение осциллятора может быть представлено в форме
dx
&x& - (l
- x2 )x& + dU (x) = 0 ,
где потенциал задан полиномом
U (x) = 1 x4 + 1 ax2 + bx + c . Такой потенциал
![]()
![]() 4 2
4 2
отвечает катастрофе сборка. Поэтому данную систему можно
назвать автоко- лебательным осциллятором
с катастрофой сборка.
Метаморфозы потенциала при вариации параметров иллюстрирует рис.15
из задачи 31. Отметим, что вдоль линии
b = 0
потенциальная функция симмет-
рична. Таким образом, в частном случае
b = 0 ,
a > 0
исследуемая система пре-
вращается в осциллятор Ван дер Поля-Дуффинга (с точностью до нормировки).
Состояния равновесия системы отвечают уравнению
x3 + ax + b = 0.
0 0
Укажем основные локальные бифуркации автоколебательного осциллятора с катастрофой сборка, для чего можно использовать результаты предыдущей
задачи. В этом случае
f (x) = x3 +
ax +
b,
g(x) = l - x2 . Опуская достаточно про-
стые выкладки, приведем соответствующие результаты.
·
Бифуркация седло-узел:
![]() 3
3
b = ±2æ- a ö 2
.
![]()
ç ÷
3
è ø
·
Бифуркация Андронова-Хопфа:
![]() b =
± (l +
a),
a > -3l.
b =
± (l +
a),
a > -3l.
Эти уравнения задают две полупрямые линии на плоскости (a,b).
·
Точки Богданова-Такенса:
a = -3l ,
3
![]() b = m2l 2 .
b = m2l 2 .
Общая картина локальных бифуркаций представлена на рис.30. На него нанесены линии седло-узловой бифуркации SN, точка сборки СР, линии бифур- каций Андронова-Хопфа АН и точки Богданова-Такенса BT.
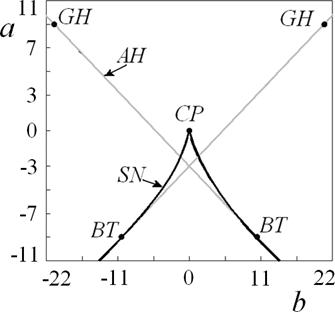
Рис.30. Картина
локальных бифуркаций автоколебательного осциллятора с катастрофой сборка для l = 3. SN –
линии седло-узловых бифуркаций, AH –
линии бифуркаций Андроно- ва-Хопфа, CP –
точка сборки, BT – точка
Богданова-Такенса, GH – точка
вырожденной би- фуркации Андронова-Хопфа.
Пример метаморфоз фазового портрета с уменьшением параметра a при
фиксированном
b = -5.5
дан на рис.31. При этом пересекаем линию бифурка-
ции Андронова-Хопфа на рис.30 сверху вниз достаточно далеко от точки сбор- ки. Вначале сосуществуют устойчивый предельный цикл и неустойчивый фо- кус. На линии бифуркации Андронова-Хопфа рождается неустойчивый пре- дельный цикл, а неподвижная точка обретает устойчивость. Дальнейшее уменьшение параметра a приводит к тому, что устойчивый и неустойчивый циклы сталкиваются и исчезают: происходит нелокальная седло-узловая бифур- кация предельного цикла. Эта бифуркация аналогична той, которая наблюдается в автогенераторе с жестким возбуждением, см. задачу 48. Соответствующая ли-
ния лежит
ниже линии бифуркации Андронова-Хопфа и заканчивается в точке контакта с
последней: в точке вырожденной бифуркации
Андронова-Хопфа GH.
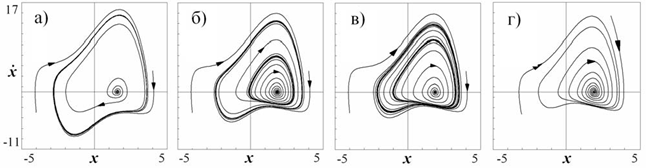
Рис.31.
Фазовые
портреты осциллятора с катастрофой сборка, построенные вдоль маршрута
b = -5.5 . Значения
второго параметра: a = 1 (а), a
= -0.4 (б), a = -0.6 (в), a
= -0.8 (г).
Выберем теперь значение
b = -3
и пересечем линию седло-узловых би-
фуркаций, а затем линию бифуркации Андронова-Хопфа в окрестности точки Богданова-Такенса (правее нее). Фазовые портреты показаны на рис.32. Снача- ла рождается пара седло и неустойчивый узел, который затем превращается в неустойчивый фокус (рис.32а). Затем происходит бифуркация Андронова- Хопфа и рождается неустойчивый предельный цикл, а фокус становится устой- чивым (рис.6б). При дальнейшем уменьшении a происходит нелокальная би- фуркация: предельный цикл влипает в сепаратрису седла и исчезает (рис.32в). В результате остаются два устойчивых фокуса и седло (рис.32г).
Полный анализ нелокальных бифуркаций можно провести, например, при
помощи пакета программ MаtCont17 . Это позволяет нанести на плоскость пара- метров (a, b) линию влипания предельного цикла в петлю сепаратрисы, которая
заканчивается в точках Богданова-Такенса, а также точки обобщенной
бифур- кации Андронова-Хопфа GH.
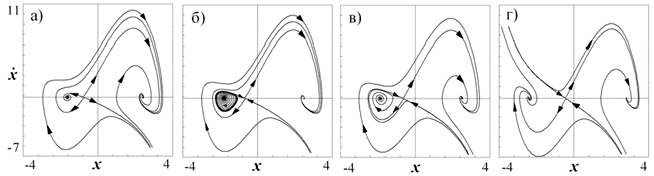
17 Пакет MatCont доступен в сети
Интернет по адресу: http://www.matcont.ugent.be и
включа- ет в себя много полезных возможностей для исследования бифуркаций
режимов динамики нелинейных систем, а именно:
нахождение точек бифуркаций, определение их принадлеж- ности к какому-либо
известному классу, способность наблюдать за динамикой бифуркаци- онных точек
при вариации параметров.
Рис.32.
Фазовые
портреты осциллятора с катастрофой сборка, построенные вдоль маршрута
b = -3 . Значения второго
параметра: a = -4.5 (а), a = -4.9 (б), a = -5.1 (в), a = -7 (г).
Мы рассмотрели осциллятор с катастрофой сборка в случае, когда потен- циал может иметь два минимума и максимум. Возможна, однако, ситуация, ко- гда потенциал задается полиномом четвертой степени, но может иметь два мак- симума и минимум между ними. Она возникает при смене знака перед старшим членом, так что
![]()
![]() U (x) = - 1 x4 + 1 ax2 + bx + c .
U (x) = - 1 x4 + 1 ax2 + bx + c .
4 2
В теории катастроф в этом
случае используют термин двойственная
сбор-
ка. Для такого потенциала уравнение автоколебательного осциллятора имеет вид
&x& - (l - x2 )x& - x3 + ax + b = 0 .
Оно может быть исследовано по аналогии с приведенным выше рассмот- рением.
52. Покажите, что
осциллятор с катастрофой сборка в случае
b = 0
описы-
вает бифуркацию коразмерности два – точку Арнольда-Такенса. Опираясь на модель в форме осциллятора, обсудите возможные режимы и бифуркации в та- кой системе.
Решение 52. Осциллятор с
катастрофой сборка при b = 0 принимает вид
&x& - (l
- x2 )x& ± x3 + ax = 0 .
При этом потенциал описывается выражением
![]()
![]() U (x) = ± 1 x4 + 1 ax2 ,
U (x) = ± 1 x4 + 1 ax2 ,
4 2
и является симметричным относительно нулевого положения равновесия. Пе- рейдем к стандартной форме уравнений:
x& = v,
v& = lv - ax m x3
- x2v.
Это соотношение является канонической моделью для точки бифуркации Арнольда-Такенса18, причем возможны два варианта этой бифуркации, которые
в соответствии со знаками обозначим
AT +
и
AT - .
Таким образом, «физическая природа» точек Арнольда-Такенса – это авто- колебательные явления в системе с симметричным двухямным (двугорбым) по-
![]()
18 Это одно из возможных названий, в литературе по теории бифуркаций используются и другие ва- рианты. Например, в математической литературе можно встретить несколько громоздкий вариант:
«два нулевых собственных значения с симметрией порядка два» [15].
тенциалом. Для систем с такой симметрией точки Арнольда-Такенса имеют ко- размерность два и, тем самым, оказываются типичными на плоскости парамет- ров. Несмотря на требование симметрии, точки такого типа оказываются суще- ственными, например, для описания картины синхронизации в резонансном случае с соотношением частот 1:2.
Обсудим сначала ситуацию, отвечающую симметричному двугорбому по- тенциалу (знак минус в выражении для потенциала). Перестройка такого по- тенциала при вариации параметра a иллюстрирует рис.33 и отвечает субкрити- ческой бифуркации вилка. Бифуркационные линии и фазовые портреты систе-
мы в окрестности точки
AT -
представлены на рис.34.
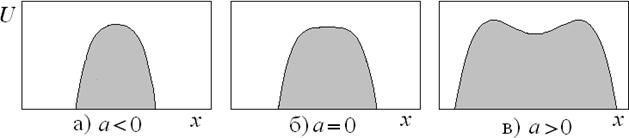
Рис.33. Метаморфозы
«двугорбого» потенциала, отвечающего за субкритическую бифурка- цию вилка.
Характерные режимы и бифуркации этой системы можно понять из физи-
ческих соображений, опираясь на условие возникновения автоколебаний
l > 0
и вид потенциала. Если
a < 0 , то при любых l в силу вида потенциала на
рис.33а, возможно одно неустойчивое равновесие – седло в начале координат.
Если
a > 0
и l < 0 , то осциллятор оказывается диссипативным, и в результате
бифуркации вилка седло становится устойчивым узлом (затем фокусом), от ко-
торого отделяются два новых седла. Наиболее интересен случай
l > 0 и
a > 0 .
При малых l возникают автоколебания, так что фокус в начале координат ста- новится неустойчивым и от него отделяется устойчивый предельный цикл. С ростом l предельный цикл растет в размере, так что неизбежно наступит мо- мент, когда он столкнется с сепаратрисами симметрично расположенных седел и исчезнет в результате соответствующей нелокальной бифуркации.
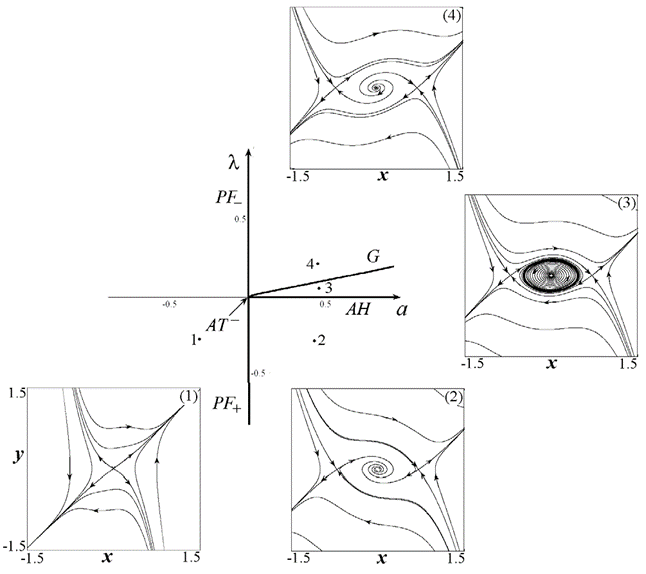
Рис.34. Бифуркационные линии
и характерные фазовые портреты в окрестности точки Ар-
нольда-Такенса
AT - . AH – линии бифуркаций Андронова-Хопфа, PF– линия бифуркации
вилка, G – нелокальная бифуркация столкновения
предельного цикла с сепаратрисами седел.
После нелокальной бифуркации остается неустойчивый фокус и два седла. Если теперь вновь уменьшать параметр a, то фокус станет неустойчивым узлом,
и на линии
a = 0
в результате бифуркации вилка он сольется с двумя седлами.
В результате, приходим к начальной ситуации, когда существует одно седло.
Таким образом, характерный «признак» точки Арнольда-Такенса
AT -
со-
стоит в том, что на плоскости параметров сходятся линии бифуркации Андро- нова-Хопфа и бифуркации вилка. В эту же точку приходит линия нелокальной бифуркации.
Обсудим теперь ситуацию, отвечающую симметричному двухямному по- тенциалу. Его перестройку иллюстрирует рис.35. Бифуркационные линии и ха- рактерные фазовые портреты в этом случае показаны на рис.36.
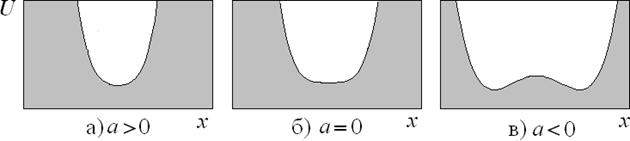
Рис.35. Метаморфозы
симметричного двухямного потенциала, отвечающего за суперкрити- ческую
бифуркацию вилка.
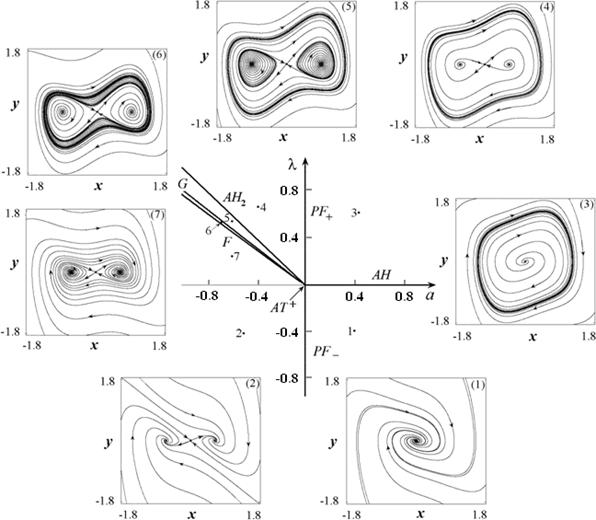
Рис.36.
Бифуркационные
линии и характерные фазовые портреты в окрестности точки Ар-
нольда-Такенса
AT + . AH – линии бифуркаций Андронова-Хопфа,
PF-
– суперкритическая
бифуркация вилка,
PF+
– субкритическая
бифуркация вилка, AH2 –
«симметричная» бифур-
кация Андронова-Хопфа, F
– касательная бифуркация предельных циклов, G – нелокальная бифуркация.
Бифуркации в этом случае также могут быть описаны с привлечением фи-
зических соображений. В области
l < 0
система представляет собой диссипа-
тивный осциллятор, и характер динамики целиком определяется перестройкой
потенциала. При
a > 0
в соответствии с рис.35а имеется устойчивое равновесие
в начале координат
x1 = 0 . Если уменьшать параметр a, то при
a = 0 устройство
потенциальной ямы изменится, равновесие в начале координат
x1 станет неус-
![]() тойчивым (седлом) и от нее отделятся два новых устойчивых равновесия.
Им
тойчивым (седлом) и от нее отделятся два новых устойчивых равновесия.
Им
отвечает минимум потенциала, так что координаты равновесий
Это тоже бифуркация вилка, но суперкритическая ее форма.
x2,3 = ± .
Пусть теперь в системе возможны автоколебания и
l > 0 . Если конфигура-
![]() ция потенциала отвечает рис.35а, то в системе имеет место классическая
для автоколебаний ситуация – устойчивый предельный цикл охватывает неустой-
чивый фокус в начале координат. Если теперь уменьшать параметр a, то пере- ход к двухямному потенциалу
приведет к бифуркации вилка этого равновесия. Поскольку оно неустойчиво, то
будет наблюдаться субкритическая бифуркация
ция потенциала отвечает рис.35а, то в системе имеет место классическая
для автоколебаний ситуация – устойчивый предельный цикл охватывает неустой-
чивый фокус в начале координат. Если теперь уменьшать параметр a, то пере- ход к двухямному потенциалу
приведет к бифуркации вилка этого равновесия. Поскольку оно неустойчиво, то
будет наблюдаться субкритическая бифуркация
рождения двух неустойчивых равновесий
x2,3 = ± .
Эти равновесия могут претерпевать бифуркацию Андронова-Хопфа рож- дения неустойчивого предельного цикла. Покажем это. Запишем матрицу ли- неаризации системы в случае верхнего знака:
æ 0 1 ö
M =
ç ÷ ,
è ø![]()
ç-
a -
3x2
- 2xy l - x2
÷
так что для неподвижных точек
x2,3 = ±
получаем
æ 0 1 ö
ø
M = ç ÷
.
è 2a l +
a
Условие бифуркации рождения предельного цикла – обращение в ноль
следа матрицы
S = l + a , так что
l = -a . Якобиан
J = -2a
и положителен при
a < 0 , как и необходимо для бифуркации Андронова-Хопфа. При этом предель-
ные циклы рождаются одновременно из обеих точек
рождение, связанное с симметрией системы.
x2,3 . Это определенное вы-
С уменьшением управляющего параметра l неустойчивые циклы сталки- ваются с ветвями сепаратрисы седла, но не исчезают, а «проходят» сквозь них, объединяясь, так что в результате этой нелокальной бифуркации возникает один неустойчивый предельный цикл, охватывающий три равновесия – седло в
начале координат и две точки
x2,3 , которые стали устойчивыми в результате
произошедшей ранее бифуркации Андронова-Хопфа.
Если и далее увеличивать параметр a или уменьшать l, то неустойчивый и устойчивый предельные циклы сближаются, сливаются и исчезают в результате fold-бифуркации. Возникает случай общего положения – два устойчивых и од- но неустойчивое равновесия, – уже обсуждавшийся выше.
Таким образом, «признак» бифуркации Арнольда-Такенса
AT +
– наличие
общей точки бифуркации Андронова-Хопфа и бифуркации вилки, которая со- стоит из двух ветвей, субкритической и суперкритической. В эту же точку при- ходит линия бифуркации Андронова-Хопфа рождения пары неустойчивых пре- дельных циклов и линия нелокальной бифуркации.
53.
Выпишите в общем виде уравнения,
задающие трехмерную потоковую динамическую систему, уравнения для состояний
равновесия этой системы и матрицу возмущений. Найдите уравнение для определения
ее собственных зна- чений через инварианты этой матрицы.
Решение 53. Трехмерная система в общем случае задается уравнениями
x& =
f (x, y, z),
y& = g(x, y, z),
z& = v(x, y, z).
Состояния равновесия нения переменных:
(x0 , y0 ,z0 )
ищем, приравнивая нулю скорости изме-
f (x0 , y0 ,z0 ) = 0,
g(x0 , y0 ,z0 ) = 0,
v(x0 , y0 , z0 ) = 0.
Динамика малых возмущений в окрестности состояния равновесия будет определяться матрицей возмущений
ç
æ f x¢
Mˆ
=
ç g¢x
f y¢
g¢y
f z¢ ö
÷
g¢z ÷ ,
ç
è v&x
v¢y
÷
v¢z ø
где соответствующие частные производные вычислены в точке равновесия
(x0 , y0 ,z0 ) .
Характеристическое уравнение этой матрицы будет кубическим, и, соот- ветственно, будет иметь три корня.
Очевидно, можно записать19:
(g - g1 )(g - g2 )(g - g3 ) = 0.
Отсюда получаем:
g3-(g1 + g2 + g3 )g2 + (g1g2 + g1g3 + g2 g3 )g - g1g2 g3 = 0,
или
g3-Sg2 + Hg - J = 0.
Входящие в это уравнение коэффициенты определяют три инварианта
матрицы
возмущений: ее след S, якобиан J и
третий инвариант H:
S = g1 + g2 + g3 , H = g1g2 + g1g3 + g2 g3 , J = g1g2 g3.
Анализ характера равновесий удобно проводить, используя инварианты матрицы в качестве параметров.
54.
Укажите возможные типичные варианты
расположения собственных чисел в случае трехмерной динамической системы на
комплексной плоскости и постройте качественно соответствующие фазовые портреты.
Решение 54. Три корня
g1,
g2 , g3
соответствующего кубического уравне-
ния могут быть либо все действительными, либо два корня
g1, g2
будут ком-
плексно сопряженными, а третий
g3 – действительным. Таким образом, по
сравнению с двумерным потоком добавляется один корень
g3 , который всегда
можно считать действительным. Это позволяет сразу дать классификацию со- стояний равновесия трехмерного потока. Для этого отмечаем, что конфигура-
ция двух корней
g1, g2
на комплексной плоскости дается рис.18. Добавление
третьего действительного корня
g3 увеличивает число вариантов в два раза, по-
скольку этот корень может быть (в типичных случаях) отрицательным или по- ложительным.
Конфигурации трех собственных чисел на комплексной плоскости и соот- ветствующие качественные фазовые портреты даны, соответственно, на рис.37 и рис.38.
![]()
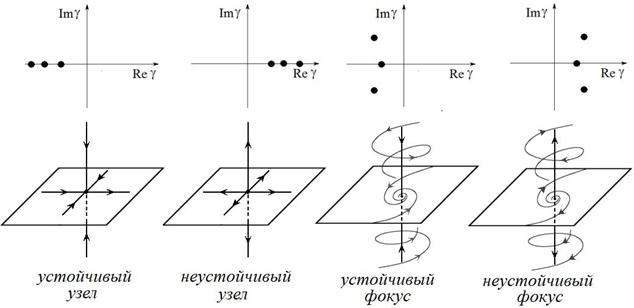
Рис.37.
Трехмерные узлы и фокусы и положение собственных чисел на
комплексной плоско- сти.
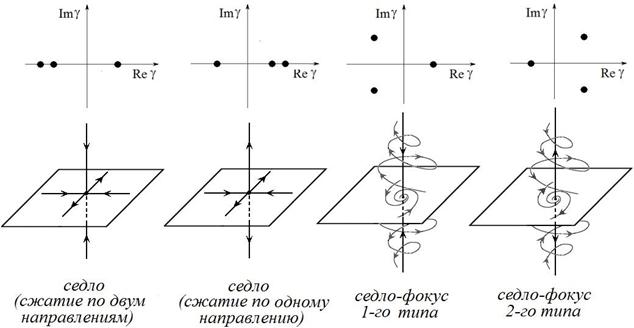
Рис.38. Трехмерные седла и седло-фокусы и положение собственных чисел на комплексной
плоскости.
Последовательно опишем возможные равновесия.
1)
Устойчивый узел. Все собственные значения
действительные и отрица-
тельные,
g1, g2 , g3 > 0 . Изображающие точки приближаются к равновесию по
всем трем направлениям.
2) Неустойчивый узел. Все собственные значения действительные и поло-
жительные,
g1, g2 , g3 < 0 . Изображающие точки убегают от равновесия по всем
трем направлениям.
3)
Устойчивый фокус. Два собственных значения комплексно-
сопряженные, и их действительная часть отрицательна, третье собственное
число отрицательное,
Re g1,,2 < 0, g3 < 0 .
4)
Неустойчивый фокус. Два собственных значения комплексно-
сопряженные, и их действительная часть положительна, третье собственное
число положительное,
Re g1,,2 > 0, g3 > 0 .
5) Седло. Все собственные значения действительные, два из них отрица-
тельные, а одно – положительное,
g1 , g2 < 0 ,
g3 > 0 . Сжатие идет по двум на-
правлениям (вдоль поверхности), а по одному – растяжение.
6)
Седло. Все собственные значения
действительные, одно из них отрица-
тельное, а два – положительные,
g1 , g2 > 0 ,
g3 < 0 . Сжатие идет по одному на-
правлению, а растяжение по двум направлениям.
7) Седло-фокус.
Два собственных значения комплексно-сопряженные, и их действительная часть
отрицательна, третье собственное число положительное, Re g1,,2 < 0,
g3 > 0 . Как говорят, седло-фокус имеет
двумерное устойчивое и од-
номерное неустойчивое многообразия. Будем называть его седло-фокусом 1-го типа.
8) Седло-фокус.
Два собственных значения комплексно-сопряженные, и их действительная часть
положительная, третье собственное число отрицательное, Re g1,,2 > 0,
g3 < 0 . Седло-фокус имеет одномерные
устойчивое и двумерное не-
устойчивое многообразия. Будем называть его седло-фокусом 2-го типа.
Устойчивый и неустойчивый узел отвечают сжатию (растяжению) сразу по всем трем направлениям. Отметим, что они переходят друг в друга при об- ращении времени.
Устойчивый фокус отвечает ситуации, когда изображающая точка при- ближается к равновесию по одному направлению, одновременно «скручива- ясь», как показано на рисунке. Неустойчивый фокус получается обращением времени.
Отметим, что при комплексных собственных числах сжатие может проте-
кать по-разному. Если
g3 < Re g1,,2 < 0 , то сначала происходит быстрое сжатие
на некоторую поверхность, а затем траектории «скручиваются» к равновесию, двигаясь по этой поверхности. В этом случае говорят, что равновесие имеет два
ведущих
направления. Если же
Re g1,,2 < g3 < 0 , то сжатие по двум направлениям
идет очень быстро. И через некоторое время точка стремится к равновесию, фактически, вдоль линии устойчивого многообразия. В этом случае говорят, что равновесие имеет одно ведущее направление.
Седло отвечает ситуации, когда по одним направлением идет сжатие, а по другим – уход траекторий от равновесия. При этом выделяются два типа седла, в зависимости от того, по одному или по двум направлениям точки сжимаются к седлу.
Седло-фокус – состояние равновесия, не имеющее аналога в двумерной системе. В этом случае траектория может «скручиваться» к равновесию вдоль поверхности, но одновременно убегать по некоторому направлению. Второй вариант седло-фокуса получается обращением времени.
55.
Найдите условие в пространстве
инвариантов матрицы возмущений, отвечающее возникновению (исчезновению)
комплексных собственных значе- ний. Обсудите характер возникающих равновесий.
Решение 55. Комплексные корни
уравнения
g3-Sg2 + Hg - J = 0
появляют-
ся, когда у функции
y(g) =g3-Sg2 + Hg - J
экстремум лежит на оси g, рис.39.
Когда экстремум «отрывается» от этой оси, действительные решения исчезают.
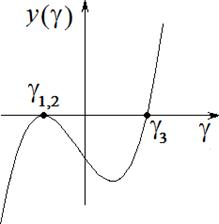
Рис.39. К
определению условия появления комплексных корней характеристического урав-
нения.
Поэтому условие появления комплексных корней имеет вид:
f (g) =g3-Sg2 + Hg - J = 0,
f ¢(g) = 3g2-2Sg + H = 0.
Второе уравнение можно решить, и решение подставить в первое, так что получаем следующее уравнение поверхности
J =g
3-Sg2
+ Hg,
g = S ± .
![]()
![]() 3
3
Его можно преобразовать к виду20:
![]() J =
1 HS -
2 S 3
± 2 (S 2 -
3H )32 .
J =
1 HS -
2 S 3
± 2 (S 2 -
3H )32 .
3 27 27
Можно отметить характерный закон «трех вторых» и возможность точки
сборки при условии
S 2 = 3H . Решения с комплексными собственными числами
могут быть фокусами или седло-фокусами.
56.
Постройте разбиение пространства
параметров инвариантов матрицы возмущений на характерные области, отвечающие
восьми грубым состояниям равновесия, показанным на рис.37,38.
Решение 56. Пространство
параметров
(S , H ,
J
)
является трехмерным.
Построим его сечения плоскостями
S = const . В первую очередь на плоскость
(H , J )
надо нанести линию
![]() J =
1 HS -
2 S 3
± 2 (S 2 -
3H )32 ,
J =
1 HS -
2 S 3
± 2 (S 2 -
3H )32 ,
3 27 27
которая разделяет области действительных и комплексных корней.
Вторая бифуркационная линия соответствует переходу пары комплексных корней из правой полуплоскости в левую (и наоборот). Чтобы ее найти, полага-
ем g = ±ia
в соотношении
g3-Sg2 + Hg - J
= 0 . Тогда получаем
J = HS, H > 0.
Еще одна характерная линия отвечает прохождению одного из собствен-
ных чисел через ноль и условию ным перестройкам.
J = 0.
Ее части отвечают нескольким возмож-
В результате приходим к следующей картине разбиения плоскости пара-
метров, показанной на рис.40. (Чтобы не загромождать рисунок типы седел и седло-фокусов не указаны – они легко идентифицируются с помощью рис.37,38.) На рис.40 хорошо видны области действительных и комплексных корней. Можно видеть также, что конфигурация бифуркационных линий при смене знака параметра S получается зеркальным отражением.
Рекомендуем самостоятельно разобраться, как в деталях соотносятся эти две диаграммы друг с другом.
![]()
20 Это уравнение
отвечает равенству нулю дискриминанта кубического уравнения.
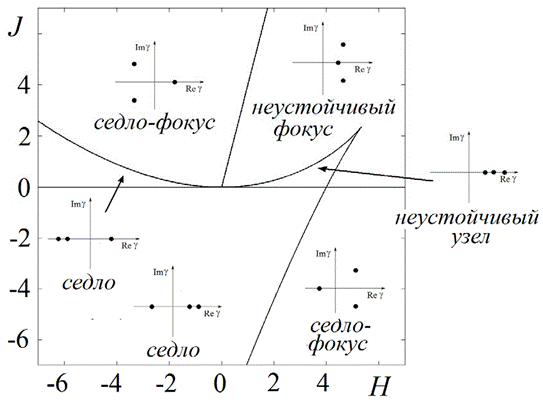
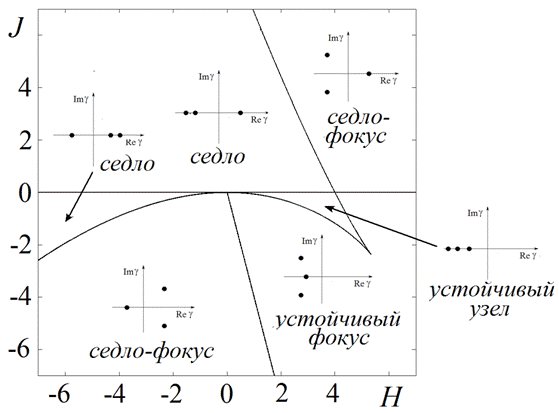
Рис.40. Конфигурации
собственных чисел для трехмерного потока в комплексной плоско- сти. Случай S=4.
Рис.40 (продолжение). Конфигурации
собственных чисел для трехмерного потока в ком- плексной плоскости. Случай S = -4 .
57. Фиксируем параметр
J = 0 , что отвечает ситуации седло-узловой би-
фуркации и определяет соответствующую плоскость в пространстве парамет- ров инвариантов матрицы возмущений. Укажите конфигурацию собственных чисел в комплексной плоскости в разных точках плоскости двух оставшихся
параметров (H , S ) . Перечислите пять ситуаций, характерных для такой ситуа-
ции. Какие варианты бифуркации седло-узел возможны в трехмерной системе?
Решение 57. Условие
J = 0
означает, что одно из собственных чисел, на-
пример,
g3 обращается в ноль. Тогда для двух оставшихся из
g3-Sg2 + Hg - J
= 0 получаем квадратное уравнение:
g2-Sg + H = 0 .
Таким образом, классификация собственных чисел
g1, g2
в этом случае
полностью аналогична рис.18 из задачи для двумерных потоков. В результате приходим к разбиению плоскости двух оставшихся параметров, показанной на рис.41, на которой изображены положения собственных чисел в характерных точках. Одно из них, в соответствии с условием, всегда находится в начале ко- ординат.
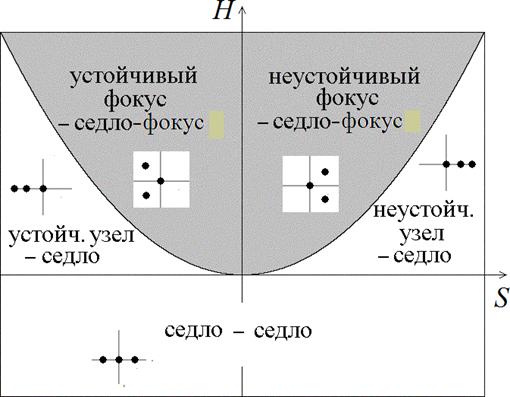
Рис.41.
Конфигурация
собственных чисел линеаризованной матрицы в случае J=0.
Обсудим теперь возможные бифуркации. Ситуации, показанные на рис.41 являются негрубыми – при малом шевелении параметра J конфигурации меня-
ются. Нетрудно понять, что при таком шевелении нулевое собственное число смещается немного влево или вправо от начала координат. Привлекая рис.37,38 получаем пять возможных вариантов.
1) Устойчивый
узел сливается с седлом с двумя сжимающими направле- ниями (седло 1-го типа).
2) Неустойчивый
узел сливается с седлом с одним сжимающим направле- нием (седло 2-го типа).
3) Устойчивый
фокус сливается с седло-фокусом 1-го типа (двумерное ус- тойчивое многообразие).
4) Неустойчивый
фокус сливается с седло-фокусом 2-го типа (одномерное устойчивое многообразие).
5) Седло
с одним сжимающим направлением сливается с седлом с двумя сжимающими направлениями.
Эти бифуркации отвечают обращению якобиана в ноль и, в определенном смысле, могут быть отнесены к седло-узловым. (Хотя, отчасти, это вопрос тер- минологии.)
58.
Какие варианты бифуркации
Андронова-Хопфа возможны в трехмер- ной системе?
Решение 58. Бифуркация Андронова-Хопфа происходит при пересечении парой комплексно-сопряженных собственных чисел мнимой оси. Как видно из рис.37,38, возможны следующие варианты:
-
а) AH - . Устойчивый фокус
превращается в седло-фокус с одним сжи-
мающим направлением. В этом случае от него отделяется устойчивый предель- ный цикл21.
-
б) AH + . Седло-фокус с
двумерным устойчивым многообразием превраща-
ется в неустойчивый фокус.
От него отделяется седловой предельный
цикл.
Отметим, что седловые предельные циклы не имеют аналога в двумерных системах. В сечении Пуанкаре такой цикл отвечает двумерному отображению с неподвижной точкой седлового типа с одним устойчивым и одним неустойчи- вым многообразиями.
Качественные фазовые портреты для этих случаев показаны на рис.42а,б.
21 В
обозначении типа бифуркации AH верхний
знак «плюс-минус» обозначает устойчивость или неустойчивость по новому,
третьему направлению. Нижний знак отвечает супер- (ми- нус) или субкритической
(плюс) бифуркации на двумерной поверхности.
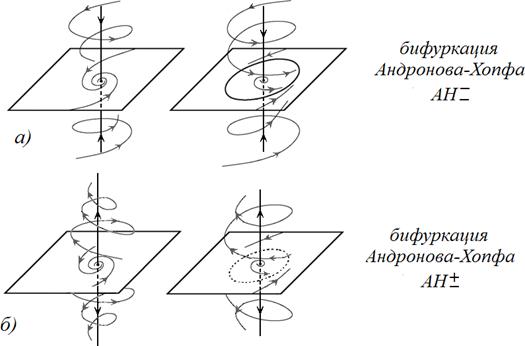
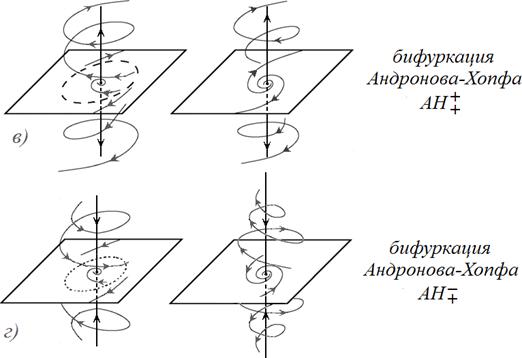
Рис.42. Разновидности
бифуркации Андронова-Хопфа трехмерных потоков. Точками пока- зан седловой
предельный цикл, пунктиром – неустойчивый.
Нетрудно видеть, что на двумерном многообразии динамика соответству- ет двумерной бифуркации Андронова-Хопфа рис.21. В обоих случаях рождает- ся устойчивый «в пределах» этой поверхности предельный цикл. Таким обра- зом, на двумерном многообразии в этих случаях имеет место суперкритическая бифуркация Андронова-Хопфа. Отличие заключается в динамике по третьему
направлению. В первом случае она сжимающая, во втором – растягивающая22. Возможны еще два варианта.
+
в) AH + . В седло-фокус с
двумерным устойчивым многообразием «влипа-
ет» неустойчивый предельный цикл. В результате возникает неустойчивый фо- кус. Ситуация получается обращением времени для случая рис.42а.
+
г) AH - . В устойчивый фокус
«влипает» седловой предельный цикл. В ре-
зультате остается седло-фокус с одним сжимающим направлением. Ситуация получается обращением времени для случая рис.42б.
Качественные фазовые портреты для этих случаев показаны на рис.42в,г. Теперь на двумерном многообразии имеем картину суперкритической двумер- ной бифуркации Андронова-Хопфа.
59.
Проведите анализ бифуркаций
состояний равновесия трехмерной ди- намической системы, используя в качестве
параметров три инварианта матрицы возмущений.
Решение 59. Уравнение для собственных значений имеет вид
g3-Sg2 + Hg - J = 0,
где инварианты матрицы возмущений, ее след S, якобиан J и третий инвари- ант H выражаются через собственные значения следующим образом:
S = g1 + g2 + g3 , H = g1g2 + g1g3 + g2 g3 , J = g1g2 g3.
Инварианты матрицы возмущений, подобно тому, как это было сделано для двумерных потоков, удобно использовать как параметры при анализе би- фуркаций. Перечислим основные бифуркации трехмерных потоков, повышая их коразмерность.
Седло-узловая бифуркация имеет коразмерность один, и поэтому ей будет
отвечать некоторая поверхность в пространстве (S, H , J ) . В этом случае одно
из собственных чисел обращается в ноль. Это означает, что ее условие
J = 0 .
Для бифуркации Андронова-Хопфа два собственных числа является чисто
мнимыми:
g1 = ia, g2 = -ia.
Подставляя эти соотношения в выражения для ин-
вариантов, получаем:
S = g3 , H =a2,
J =a2g3.
Таким образом, условие бифуркации Андронова-Хопфа имеет вид:
22 В
использованных обозначениях нижний индекс отвечает супер- и субкритическим фор-
мам бифуркации Андронова-Хопфа на двумерном многообразии. Верхний индекс
отвечает за знак нового, третьего направления.
J = HS, H > 0.
Это тоже бифуркация коразмерности один, и ей будет отвечать соответст- вующая поверхность в пространстве параметров.
Третье собственное число для бифуркации Андронова-Хопфа совпадает со
следом матрицы. Поэтому при
S < 0
третье направление оказывается устойчи-
вым, а при
S > 0
- неустойчивым. Таким образом, при
S < 0
будет рождаться
траектории приближаются к нему по некоторой поверхности, но уходят от него по третьему направлению.
Бифуркация Богданова-Такенса имеет коразмерность два, и ей будет отве- чать некоторая линия в пространстве параметров. Ее уравнение находим из ус-
ловия, что два собственных числа сливаются и обращаются в ноль:
Тогда из выражений для инвариантов получаем
g1 = g2
= 0 .
J = 0, H = 0.
При этом третье собственное число совпадает со следом матрицы.
Для трехмерной системы появляется новая бифуркация коразмерности два. Действительно, для нее может выполняться как условие бифуркации Андроно- ва-Хопфа, так и седло-узловой бифуркации, но за счет обращения в ноль до- полнительного третьего собственного числа. Такую бифуркацию называют
J = 0, S = 0, H > 0 .
Наконец, при условии
J = S = H = 0
все три собственных числа обращают-
ся в ноль, что дает точку коразмерности три.
Конфигурацию бифуркаций удобно проследить в сечении
H = const , при-
чем при
H > 0 . Такое сечение показано на рис.43.
Картина в трехмерном пространстве параметров (S, H , J ) дана на рис.44. В
этом случае седло-узловая бифуркация дается плоскостью
J = 0 . Ее пересече-
ние с плоскостью бифуркации Андронова-Хопфа AH дает линию «седло-узел- Хопф» SNH и линию Богданова-Такенса BT. В свою очередь, эти линии пересе- каются в точке коразмерности три – начале координат. Причем, линия SNH за- канчивается в этой точке. На рисунке показана только часть поверхности би-
![]()
23 Здесь рассматриваем вариант прямой
бифуркации Андронова-Хопфа. Возможна, однако, и суперкритическая форма, которой
отвечает возникновение неустойчивого предельного цик-
ла.
фуркации Андронова-Хопфа
AH + . Вторая ее часть
AH -
располагается под
плоскостью седло-узловой бифуркации симметричным образом в области от- рицательных S, см. рис.43.
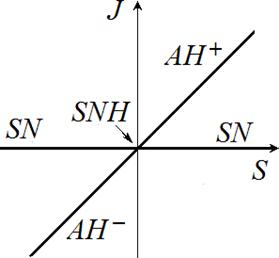
Рис.43. Линии
и точки основных бифуркаций равновесия трехмерного потока на плоскости (S,J) при H=1; бифуркация Андронова-Хопфа AH,
седло-узел SN, точка седло-узел-Хопф SNH.
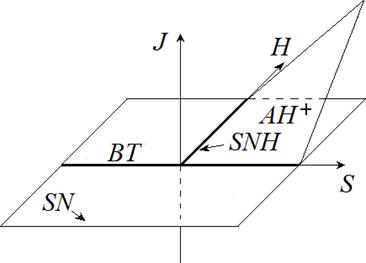
Рис.44. Поверхности
и линии основных бифуркаций равновесия трехмерного потока в про- странстве
инвариантов матрицы возмущений (S,J,H)
.
60.
Для одной из базовых моделей нелинейной динамики – системы Ресс-
лера
x& = - y - z, y& = x + py,
z& = q + (x - r)z,
найдите два возможных состояния равновесия и укажите условие, когда они сливаются в результате седло-узловой бифуркации. Установите, при каком ус- ловии в этом случае рождается устойчивое равновесие. (Для определенности
считаем, что
p > 0.)
![]() Решение 60. Состояния
равновесия системы Ресслера даются соотноше- ниями:
Решение 60. Состояния
равновесия системы Ресслера даются соотноше- ниями:
x0 = pz0 ,
y0 = -z0 ,
z0 = 2 p .
r![]()
Таким образом, возможны два состояния
равновесия, причем из аналити- ческого выражения очевидно, что они сливаются и
исчезают при условии
r 2 - 4 pq = 0 . При этом в точке бифуркации
z0 = 2 p .
r![]()
Фиксируем это бифуркационное условие, и
записываем матрицу возму-
щений для состояния равновесия с учетом
z0 = 2 p :
æ 0 -1
-1 ö
ç ÷
Mˆ = ç 1 p 0 ÷ .
è ø
ç z0 0 - pz0 ÷
Выписываем характеристическое уравнение ничная матрица. Тогда получаем
det(Mˆ - gEˆ) = 0 , где Eˆ – еди-
0
g3- p(1- z0 )g2
+ (z -
p2
z0
+1)g = 0.
![]()
![]() Как и следовало ожидать, якобиан равен нулю, поскольку мы фиксировали
условие слияния двух корней. Оставшиеся инварианты:
Как и следовало ожидать, якобиан равен нулю, поскольку мы фиксировали
условие слияния двух корней. Оставшиеся инварианты:
S = p(1- z0 )
=
p - r ,
![]() 2
2
H = z0
- p2
z0
+1 =
r - rp +1. 2 p 2
Теперь можно применить результаты решения задачи 57.
Возникающее равновесие будет устойчивым, если ляя сюда выражения для следа и якобиана, получаем:
r( p2 -1)
S < 0, H
> 0 . Подстав-
r > 2 p ,
< 2.
![]() p
p
По условию
p > 0.
Поэтому второе неравенство при
p < 1 выполняется ав-
томатически. При
p > 1 его можно переписать, как
r < r0 =
2 p .
![]() p2 -1
p2 -1
При этом оба
неравенства одновременно имеют решения, если
2 p < r0 ,
что приводит к
![]() p < 2 . Таким образом, устойчивое
равновесие рождается при следующих ус-
p < 2 . Таким образом, устойчивое
равновесие рождается при следующих ус-
ловиях:
0 < p £ 1,
r > 2 p ,
![]() 1 < p <
1 < p <
, 2 p < r <
2 p ,
![]() p2 -1
p2 -1
![]() p > , решений нет.
p > , решений нет.
Пусть, например,
0 < p £ 1. Вспоминая, что мы наложили условие бифур-
кации седло-узел
r 2 = 4 pq , получаем, что при фиксированном q условие ус-
тойчивости решения
r > 2 p
означает
p < q .
Рекомендуем самостоятельно отличить случаи устойчивого узла и фокуса.
61.
Найдите порог бифуркации
Андронова–Хопфа в трехмерном потоке, описывающем генератор Кислова–Дмитриева.
Этот генератор состоит из трех замкнутых в кольцо элементов: нелинейного
усилителя НУ, инерционного эле- мента ИЭ и фильтра Ф в виде колебательного
контура, рис. 45. Для усилителя предполагается, что сигналы на входе и выходе
связаны через функцию
F (z) = Mze-z2 .
Такая система описывается трехмерным потоком
x& = - x / T
+ F (z) / T ,
y& = x - z,
z& = y - z / Q.
Здесь М — коэффициент усиления, Q — добротность контура, Т — характерное время инерционного элемента. Покажите, что порог бифуркации Андронова– Хопфа дается соотношением
æ T öæ 1 ö
2 ln M
= ç1+ ÷ç1+ ÷.
![]()
![]() Q QT
Q QT
è øè ø
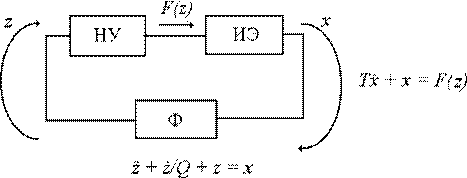
Рис.45. Функциональная схема генератора
Кислова-Дмитриева.
Решение 61. В системе есть тривиальное равновесие, которое при
M = 1 в
![]() результате бифуркации вилка становится неустойчивым, и от него
отделяется пара устойчивых равновесий, так что
результате бифуркации вилка становится неустойчивым, и от него
отделяется пара устойчивых равновесий, так что
x0 =z0 ,
y0 =z0 / Q,
z0 =
ln M .
(Мы оставили решение с положительным z, имеющее физический смысл.) На- ходим матрицу возмущения в этой точке:
1
æ
![]() ç-
ç-
ç T
Mˆ = ç 1
ç
ç
ç 0
è
0 F ¢(z0 ) ö
÷![]()
T ÷
0 -1 ÷ ,
÷
÷![]()
1 - 1 ÷
Q ø
где
F ¢(z0 ) = 1- 2z 2 = 1- 2 ln M . Выписываем характеристическое уравнение
0
det(Mˆ - gEˆ) = 0 , где Eˆ – единичная матрица. Тогда получаем:
3 æ 1
1 ö 2 æ
1 ö 2 ln M
![]() g -ç
g -ç
T
+ ÷g
![]() Q
Q
+ ç1+ ÷g +
![]()
![]() Q T
Q T
= 0.
Отсюда следует, что
è ø è ø
![]()
![]() S = - 1 - 1 ,
S = - 1 - 1 ,
H = 1 +
1
, J
= - 2 ln
M .
![]()
![]() T Q TQ T
T Q TQ T
Мы нашли связь параметров системы с инвариантами матрицы. Теперь можно воспользоваться готовым соотношением для бифуркации Андронова-
Хопфа
J = HS , так что получаем
æ T öæ 1 ö
2 ln M
= ç1+ ÷ç1+ ÷.
![]()
![]() Q QT
Q QT
è øè ø
Отметим, что
H > 0 , так что второе условие бифуркации Андронова-
Хопфа выполнено. Из полученного соотношения можно получить значение ко- эффициента усиления M для заданных добротности и времени задержки, отве- чающее возникновению автоколебаний в результате бифуркации Андронова- Хопфа.
62.
Для модели Рёсслера следующего вида25
x& = - y - z,
y& = x +
ay, ,
z& = bx + (x - c)z,
25 Такой вариант модели Рёсслера
рассмотрен в книге Г. Николис, И. Пригожин. Познание сложного, 1990. М.: Мир,
345 с.
найдите связь между параметрами, соответствующую бифуркации Андронова– Хопфа неподвижной точки x=y=z=0. Найдите условие бифуркации «седло- узел-Хопф».
Решение 62. Действуем аналогично предыдущей задаче, и получаем ха- рактеристическое уравнение
g3-(a - с)g2 + (1+ b - ac)g + c - ba = 0.
Это означает, что
S = a - c,
H = 1 + b -
ac, J
= ba - c.
Таким образом, условия бифуркации Андронова-Хопфа
J = HS,
H > 0
приводят к
b =
a +
ac -
a2
,
![]() c
c
a2 - a < 1.
![]() c
c
Отметим, что якобиан может обратиться в ноль, если
c = ab . В этой точке
тривиальное равновесие сливается с другим равновесием:
x0 = -ab,
y0 = b,
z = c - b , но ни то, ни другое не исчезают, так что это не сед-
![]() 0 a
0 a
ло-узловая бифуркация, а вырожденная ситуация.
Компьютерное исследование трехмерных потоков
63. Для системы Ресслера
на плоскости параметров
( p, r)
x& = - y - z, y& = x + py,
z& = q + (x - r)z,
постройте численно карту динамических режи-
мов, на которой разными цветами покажите области периодических режимов, которым отвечает определенный период цикла в сечении Пуанкаре. Выберите q = 0.2 . Постройте также характерные фазовые портреты в избранных точках
плоскости параметров.
Решение 63. Полученные численно карта режимов и фазовые портреты показаны на рис.46.
На примере системы Ресслера можно наблюдать каскад бифуркаций уд- воения периода. Первоначально существует однооборотный предельный цикл (правый нижний угол рисунка), которому отвечает неподвижная точка в сече- нии Пуанкаре. Затем цикл превращается в «двухоборотный», и в сечении Пуан- каре наблюдается 2-цикл, и т.д. с возникновением хаоса. В области хаоса на- блюдаются окна устойчивости, для которых характерны разные типы предель-
ных циклов. Отметим, что здесь и в следующей задаче области хаоса показаны белым цветом – в этом случае лучше видны окна регулярных режимов в хаосе. Наиболее широкому окну отвечает период 3 в сечении Пуанкаре. Характерным на плоскости параметров является также наличие областей типа crossroad-area.
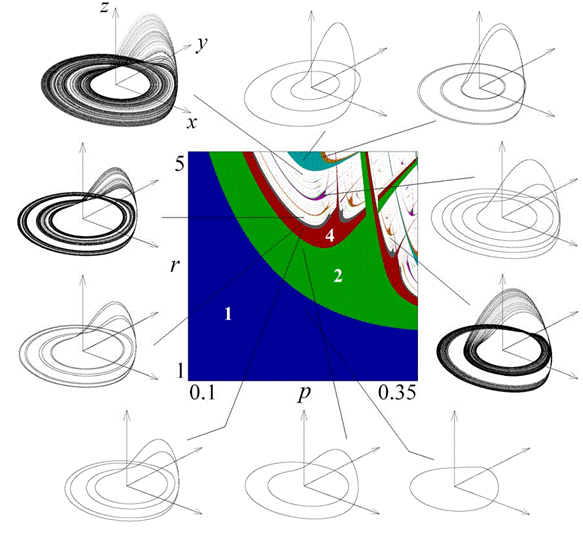
Рис.46. Карта динамических режимов
и фазовые портреты для системы Ресслера, q=0.2.
64.
Используя сечение Пуанкаре,
постройте для системы Ресслера зависи- мость
одной из переменных x в этом сечении
от управляющего параметра
p
–
бифуркационное дерево. Значения
q = 0.1, r = 8.5.
Решение 64. Полученное бифуркационное дерево дано на рис.47. Можно видеть интервалы, в которых существуют циклы различных периодов: 1, 2, 4, 8 и т.д., 3, 6, 12 и т.д. Можно видеть, что имеет место переход к хаосу по Фейген- баумовскому сценарию через каскад бифуркаций удвоения периода.
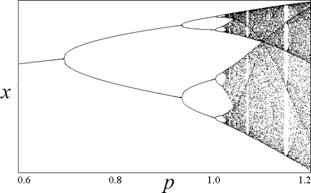 Рис.47. Бифуркационное дерево системы
Рис.47. Бифуркационное дерево системы
Рёсслера для значений параметров
r = 8.5.
q = 0.1,
65. Генератор Анищенко-Астахова описывается уравнениями
x& = mx + y - xz,
y& = -x,
z& = -gz +1(x)x2.
Постройте карту динамических режимов этого генератора.
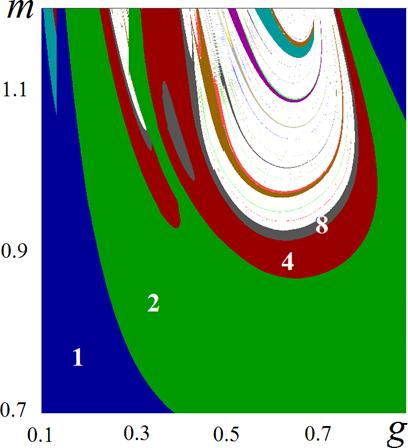
Решение 65. Решение иллюстрирует рис.48. Можно видеть характерные элементы
плоскости параметров.
Рис.48.
Карта
режимов генератора Анищенко-Астахова.
66.
Одна из моделей динамики нейрона
известна как система Хиндмарш- Розе (Hindmarsh-Rose):
x& = y - z - x3 + 3x2+I ,
y& = 1- y - 5x2 ,
z&
= r(4(x +1.6) -
z).
Здесь x описывает мембранный потенциал нейрона, y и z определяют динамику ионных токов, I – внешний ток, r – параметр. Для нейронной динамики следу-
ет считать
r << 1. (Типичное значение порядка 0.003.) Постройте карту динами-
ческих режимов на плоскости (I , r) . Приведите примеры реализаций.
Решение 66. Решение иллюстрирует рис.49. Можно видеть, что в некото- рых областях параметров система демонстрирует нейроподобную динамику – реализации содержат спайки и берсты. С ростом параметра r эта особенность реализаций исчезает.
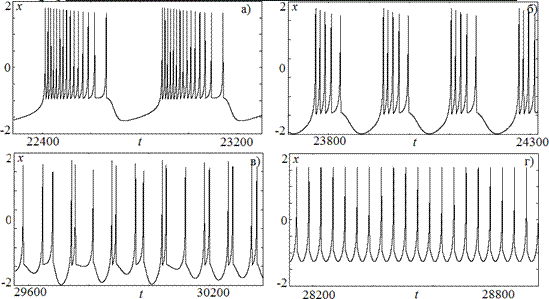
Рис.49. Карта динамических
режимов системы Хиндмарш-Розе и примеры реализаций. Па-
раметры:
r=0.033
a = 3, b = 1, c = 1, d = 5, s = 4, x0 = -1.6 , I=2.7, а) r=0.001, б) r=0.004, в) r=0.012, г)
67. Дайте
качественную иллюстрацию связи картины инвариантного тора и его сечения
Пуанкаре. Как будут выглядеть ситуации резонансного предельно- го цикла,
возникшего на этом торе? Что будет в случае разрушающегося тора?
Решение 67. Соответствующие иллюстрации получается при построении сечения Пуанкаре, рис.50.
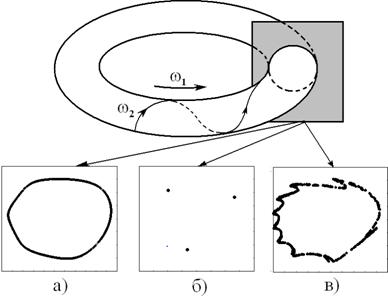
Рис.50. Инвариантный тор и
его сечение Пуанкаре (а), резонансный предельный цикл на то-
ре в сечении Пуанкаре (б), разрушающаяся
инвариантная кривая (в). w1 и w2
– частоты.
68.
Рассмотрите модель генератора
квазипериодических колебаний, пред- ставляющего собой «гибрид» автогенератора с
жестким возбуждением и релак- сационного генератора26:
&x& - (l + z + x2 - 1 x4 )x& + w2 x = 0,
![]()
2 0
z& = m - x2.
Здесь w0
– собственная частота
генератора, λ характеризует отрицательное
тре-
ние, член четвертой степени отвечает за насыщение колебаний при больших амплитудах. Параметр λ входит в уравнение вместе с аддитивной добавкой z , которая характеризует состояние накопительного релаксационного элемента, а эволюция этой переменной во времени задается вторым уравнением. Система характеризуется двумя временными масштабами: основной период колебаний
автогенератора
T = 2p / w0
и характерное время восстановления состояния на-
![]()
26
Предложен в А.П. Кузнецов, С.П. Кузнецов, Н.В. Станкевич. Известия вузов –
Прикладная нелинейная динамика, 2010, №2, с. 51.
копительного элемента
t ~ m-1. Постройте реализацию для динамических пере-
менных x и z, фазовый портрет в трехмерном фазовом пространстве и фурье-
спектр для
l = 0 , w0 = 2p , m = 0.5 .
Решение 68. При выбранных значениях параметров система демонстриру- ет автономные квазипериодические колебания. Эти особенности хорошо видны
на реализации
x(t)
в виде характерных биений, рис.51а. Реализация
z(t)
демон-
стрирует динамику типа накопление-сброс. Фазовый портрет в трехмерном пространстве представляет собой инвариантный тор, рис.51б. Фурье-спектр да- ет набор линий, характерный для квазипериодических колебаний, рис.51в. Он содержит дискретное множество равноудаленных друг от друга частотных компонент. Амплитуда компонент уменьшается вправо и влево от главной спектральной составляющей, которая соответствует основной частоте автоко-
лебательного элемента; в рассматриваемом случае
f0 = w0 / 2p = 1.
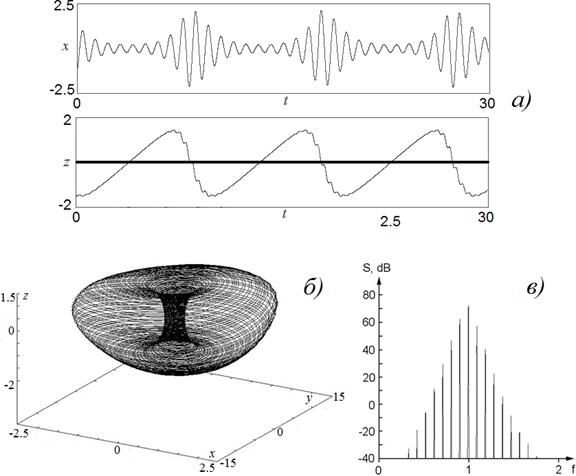
Рис.51. Реализации
(а), фазовый портрет (б) и фурье-спектр (в) квазипериодических колеба- ний при l = 0
, w0 = 2p , m = 0.5 .
Размерность четыре
69. Для модифицированной
четырехмерной системы Лоренца27
x& = a( y - x) + eyz,
y& = cx - dxz + y + u,
z& = xy - bz,
u& = -ky,
с помощью расчета спектра показателей Ляпунова продемонстрируйте возмож- ность гиперхаоса с двумя положительными показателями. Значения параметров
a = 35, c = 25, d = 5, e = 35, k = 100 . Какие еще режимы возможны в системе?
Решение 69. На рис.52 показаны графики ляпуновских показателей и ха- рактерные примеры аттракторов. Можно видеть, что в системе возможен как хаос, так и гиперхаос. Интересная особенность системы состоит в том, что в ней возможны автономные квазипериодические колебания.
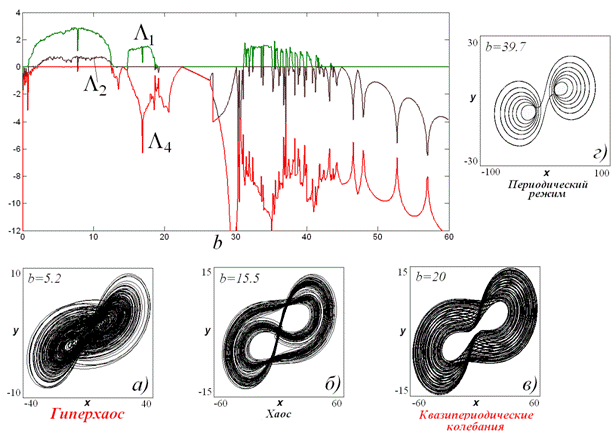
Рис.52. Ляпуновские
показатели системы с гиперхаосом и квазипериодичностью (ляпунов-
ский показатель L3 » 0
на графике не указан).
70.
Для модифицированного генератора Анищенко-Астахова, описываемо- го уравнениями
x& = mx + y - xj - dx3,
y& = -x, z& = j,
j& = -gj + g1(x)x2 - gz,
продемонстрируйте возможность бифуркации удвоения инвариантного тора. Здесь m – параметр возбуждения, d – параметр нелинейной диссипации, g – па- раметр затухания и g – параметр инерционности фильтра.
Решение 70. Зафиксируем параметры следующим образом:
g = 0.2 ,
d=0.001, g=0.5. На рис.53 представлены проекции аттракторов в сечении Пуан- каре на плоскость (y,z) при постепенном увеличении параметра m. Как видно из рисунка, при m=0.067 (рис.53б) инвариантная кривая становится двухоборотной
–
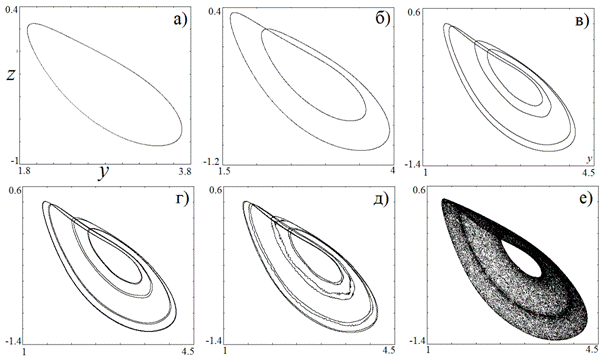
данная перестройка соответствует бифуркации
удвоения тора. При дальней- шем увеличении параметра m можно наблюдать еще две бифуркации удвоения тора. Далее
инвариантная кривая теряет гладкость, и реализуется переход к хаосу через ее разрушение.
Рис.53. Двумерные
проекции сечения Пуанкаре модифицированного генератора Анищенко- Астахова для
параметров g=0.2, d=0.001, g=0.5: а) m=0.065; б) m=0.067; в) m=0.068; г) m=0.0689; д) m=0.069; е) m=0.073.
Бифуркации одномерных отображений коразмерности один
71.
Простейшей моделью в виде одномерного отображения со
сложной ди-
намикой является логистическое
отображение
xn+1 =
f (xn ) = 1 - lx2.
Найдите
n 0
его неподвижную точку и область ее устойчивости.
Решение 71. Для неподвижной точки
x0 =
1- lx2
,
откуда следует
![]() x = -1±
x = -1±
0 2l
. Вычисляем мультипликатор:
m = f ¢(x0
) = -2lx0
= 1 m
1 + 4l.
![]() Область устойчивости отвечает условию
Область устойчивости отвечает условию
-1 < m < +1, причем нижняя граница
соответствует касательной бифуркации, а верхняя – бифуркации удвоения пе-
![]()
![]() риода. Отсюда для случая верхнего знака следует - 1 < l < 3 .
риода. Отсюда для случая верхнего знака следует - 1 < l < 3 .
Нижний знак от-
4 4
вечает всегда неустойчивой точке.
72. Для отображения
xn+1 =
l
x
f (xn ) =
n
+
xn -1
найдите неподвижную точ-
ку, зависимость ее мультипликатора от параметра
m(l)
и значение параметра
l1 , отвечающее первой бифуркации удвоения. Найдите элементы 2-цикла. Най-
дите мультипликатор 2-цикла в зависимости от параметра
m2 (l) . Найдите точ-
ку l2
бифуркации удвоения 2-цикла.
Решение 72. Неподвижную точку ищем из уравнения
x0 =
f (x0 ) :
x0 =
l
+
x![]()
x0
0
-1, откуда следует
x0 = l.
Мультипликатор в неподвижной точке
m = f ¢(x ) = - l +1 = 1- 1 .
![]()
![]()
x l
0 2
0
Таким образом, первая бифуркация удвоения периода отвечает значению
m = -1, откуда следует
l = 1 ,
![]() 1 2
1 2
причем
x = 1 .
![]() 0 2
0 2
Элементы два-цикла отображения ищем из уравнений
x2 =
1
x =
l
+
x![]()
x1
1
l + x
![]()
-1,
-1.
x
2
2
Вычитая эти уравнения друг из друга с учетом
x ¹ x , получаем x x = l .
![]()
2 1 1
2 2
Складывая их, находим
l
![]() x2 + x1
= x x
x2 + x1
= x x
(x2
+ x1 ) +
(x2
+ x1 ) -
2.
Отсюда следует, что
2 1
x2 + x1 = 1. Элементы 2-цикла ищем по теореме Виета из уравнения
Отсюда следует, что
x2
- x +
l
![]() 2
2
= 0 .
![]() x = 1 ±
x = 1 ±
![]()
1 - l .
В момент рождения 2-цикла
1,2
l
2
= 1 , x
![]()
4 2
= 1 ,
![]()
что согласуется с предыду-
щими результатами.
Мультипликатор 2-цикла
1 2 1,2 2
æ l öæ l ö
![]()
![]()
(x1 + x2 )2 - 2x1x2 - l
![]()
m2 =
f ¢(x1 ) f
¢(x2 ) = ç1- x2 ÷ç1- x2 ÷ = 1-
(x x )2 l.
è 1 øè 2 ø 1 2
С учетом полученных выражений для элементов цикла, находим:
![]() m = 9l - 4 .
m = 9l - 4 .
2 l
В точке рождения 2-цикла
l = 1
![]() 1 2
1 2
получаем
m2 = +1, как и должно быть.
Бифуркацию удвоения 2-цикла ищем, полагая
m2 = -1. Отсюда находим:
![]() l = 2 .
l = 2 .
2 5
73.
Постройте численно бифуркационное дерево для
логистического ото-
бражения
xn+1 = 1- lx2 . Постройте график ляпуновского показателя в зависимо-
n
сти от управляющего параметра.
Решение 73. Решение иллюстрирует рис.54а, на котором виден каскад би- фуркаций удвоения периода и области хаоса с окнами регулярной динамики.
График ляпуновского показателя представлен на рис.54б. Можно видеть области регулярных режимов с отрицательным показателем Ляпунова, а также области хаоса, где значения показателя положительны. Указана критическая точка
lс = 1.401155189092...,
выше которой становится возможен хаос.
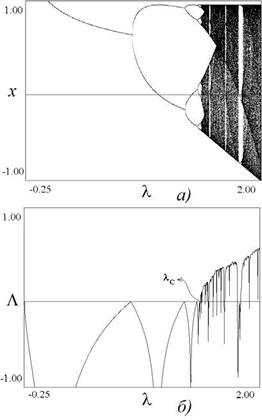
Рис.54. Бифуркационное
дерево логистического отображения и график ляпуновского показа- теля в
зависимости от параметра.
74.
Получите уравнения, определяющие
значения переменной x и бифур-
кационные значения параметра
l для касательной бифуркации неподвижных
точек отображения
xn+1 = lcos xn . Покажите, что существует множество таких
бифуркаций. Приближенно оцените соответствующие значения параметра l .
Проделайте то же самое для бифуркации удвоения периода.
Решение 74. Уравнение для поиска неподвижных точек
Мультипликатор
x0 = lcos x0 .
m = f ¢(x0 ) = -l sin x0 .
Условие касательной бифуркации
m = -l sin x0 = +1. Таким образом,
сtgx0 = -x0 . Рекомендуем дать графическую иллюстрацию решения этого урав-
нения. Асимптотически решения стремятся к
x0 = p + np . Соответственно,
l1 = ± x0 . Для бифуркации удвоения решение аналогично.
75. Для отображения
xn+1
=l + x
- x2
,
описывающего касательную бифур-
n n
кацию, оцените число итераций,
необходимое для прохождения «коридора»
вблизи порога бифуркации
x0 = -1, а конечное – xo=1.
l = -0.0001. Начальное значение переменной
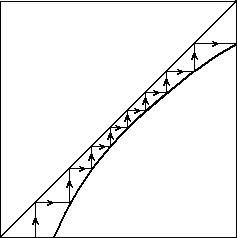
Решение 75. В представленном случае динамика в дискретном времени замедляется,
значения переменной на разных итерациях близки друг к другу, рис.55.
Рис.55.
Движение
изображающей точки вблизи порога касательной бифуркации
Поэтому можно положить
xn+1
- xn
= dx , где t – непрерывная переменная,
![]() dt
dt
своего рода медленное время. В результате получаем
![]() dx
= l - x2 .
dx
= l - x2 .
dt
Решая это уравнение при
l < 0 , находим
![]() t = 2
t = 2
arctg
x0 .
![]() При
При
l = -0.001
тригонометрическая функция стремится к значению p и
![]() 2
2
перестает зависеть от начального значения переменной: основной вклад вносит движение по «коридору». Таким образом,
В нашем случае t »
t » .
![]()
![]() » 314.
» 314.
76. Покажите, что для отображения
xn+1
= lxn
имеет место бифур-
![]()
![]() кация типа «вилка». Найдите бифуркационное значение параметра и
изобразите итерационные диаграммы для ситуаций до и после бифуркации.
кация типа «вилка». Найдите бифуркационное значение параметра и
изобразите итерационные диаграммы для ситуаций до и после бифуркации.
![]() Решение 76. Уравнение для
поиска неподвижных точек Отсюда следует, что есть решения:
Решение 76. Уравнение для
поиска неподвижных точек Отсюда следует, что есть решения:
x0 = lx0 / .
x0 = 0 и x0 =
±l / .
Таким образом, при
l > 1 возникает новая пара решений. Нетрудно вычис-
лить мультипликатор, для которого
m = 1
![]() l2
l2
. При
l = 1
мультипликатор обраща-
ется в +1. С учетом появления пары новых решений, это отвечает бифуркации вилка.
77.
Для логистического отображения
изобразите итерационные диаграм- мы, иллюстрирующие основные возможные режимы.
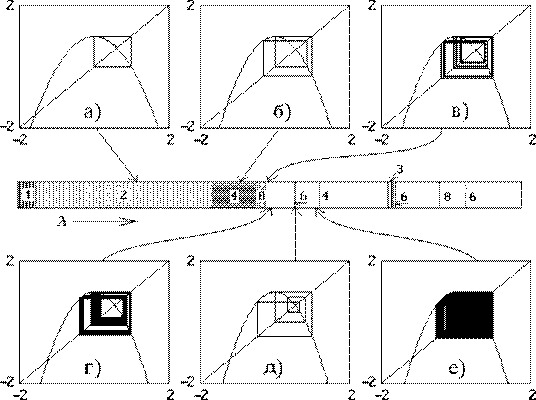
Решение 77. Итерационные диаграммы приведены на рис.56. Показаны 2- цикл и 4-цикл
максимальной устойчивости, аттрактор в критической точке, два вида хаотических
режимов и цикл период 3 в закритической области.
Рис.56. Расположение
некоторых характерных режимов на итерационной диаграмме в раз- ных точках на
оси управляющего параметра l.
78.
Получите уравнение, с помощью
которого можно найти 3-цикл макси- мальной устойчивости логистического отображения.
Решение 78. Один из элементов цикла опирается на экстремум ловие максимальной устойчивости). Поэтому
x = 0
(ус-
x = 0 , x = f (x ) = 1, x = 1 - l, x
= 1 - l(1 - l)2.
1 2 1 3 4
Условие цикла периода 3 – это
x1 = x4 ,
так что 1 - l(1 - l)2 = 0.
Таким об-
разом, получилось кубическое уравнение относительно параметра отображения.
79.
Для логистического отображения
постройте итерационные диаграммы для всех возможных типов 3-циклов, 4-циклов и
5-циклов в закритической об- ласти.
Решение 79. Итерационные диаграммы приведены на рис.57. Использова- ны значения параметра, отвечающее сверхустойчивым циклам – все они опи- раются на квадратичный экстремум. Такие циклы наиболее удобны при по- строении итерационной диаграммы на компьютере.
|
период
3 |
период
4 |
|
период
5 |
|
|
период
6 |
|
Рис.57.
Циклы
разных периодов логистического отображения в закритической области.
80. Постройте функцию
F ( x) =
f ( f ( x)),
где
f (x) = 1- lx2 . Изобразите её
график при различных l и обсудите его трансформации у порога бифуркации рождения 2-цикла логистического отображения. Укажите элементы 2-цикла на этом рисунке.
Решение 80. Двукратно проитерированное логистическое отображение ха- рактеризуется функцией
F (x) = 1- l(1- lx2 )2 = 1- l + 2l2x2 - l3x4 ,
являющейся полиномом четвертой степени. Трансформации функции F (x),
происходящие вблизи точки удвоения периода l = 0.75 , показаны на рис.58.
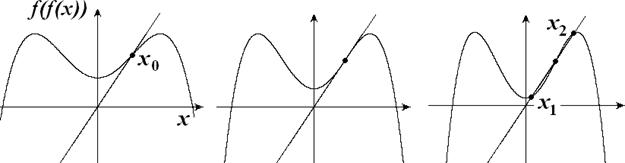
Рис.58.
Функция,
задающая двукратно проитерированное логистическое отображение при
бифуркации удвоения периода; x0
– устойчивая
неподвижная точка исходного отображения,
x1 и x2 – элементы 2-цикла исходного отображения.
Эволюция функции на рис.58 отвечает бифуркации «вилка»: одна из не- подвижных точек теряет устойчивость, и от нее отделяются две устойчивые. Для них
F (x) = f ( f
(x)) = x .
Они представляют собой элементы 2-цикла исходного отображения:
x2 =
f (x1 )
и x1 =
f (x2 ) .
81.
Покажите, что если
отображение
xn+1 =
f (
xn )
имеет неподвижную точ-
ку x0, в которой мультипликатор обращается в минус единицу:
m=
f ¢(
x0 )
= -1,
то двукратно проитерированное отображение
дующими свойствами:
F ( x0 ) =
f (
f ( x0 ))
обладает сле-
1. F ¢( x0 )
= +1 ;
2.
F ¢¢( x0 ) = 0 ;
f ¢¢¢ 3 æ f ¢¢ ö2
3. F ¢¢¢(
x0 ) = 2Sf (
x0 ) , где
Sf =
f ¢ - 2 ç
f ¢ ÷
— так
называемая производная
![]()
![]()
![]() è ø
è ø
Шварца
функции
f.
Решение 81. Во-первых, по правилу дифференцирования сложной функ- ции имеем:
F¢(x) = f ¢( f (x)) × f ¢(x) = [ f ¢(x)]2 = (-1)2 = +1,
поскольку точки.)
f ¢(x) = -1. (Для сокращения записи опускаем индекс у неподвижной
Во-вторых, вычисляя
F¢ (x) , получаем
поскольку
F ¢ (x) =
f ¢ ( f (x)) ×[ f ¢(x)]2 +
f ¢(
f (x)) ×
f ¢ (x) =
f ¢ (x) -
f ¢ (x) = 0 ,
f (x) = x и f ¢(x) = -1.
Наконец, вычисляем третью производную
F ¢¢(x) . Опять используем пра-
вила дифференцирования сложной функции, и получаем
F ¢¢(x) =
f ¢¢( f (x)) ×[ f ¢(x)]3 + 3 f ¢(x)
× f ¢ ( f (x)) ×
f ¢ (x) +
f ¢( f (x)) f ¢¢(x) .
Используя полученные выше соотношения, приходим к уравнению
F ¢¢(x) = -2 f ¢¢(x) - 3 × [ f ¢ (x)]2 .
В свою очередь, для производной Шварца в анализируемой точке имеем
Sf (x) =
Таким образом,
f ¢¢(x) - 3 æ
ç![]()
f ¢(x) 2 è
f ¢ (x) ö2
ø![]()
f ¢(x) ÷
= - f ¢¢(x) -
3 [ f ¢ (x)]2 .
![]() 2
2
F ¢¢(x) = 2Sf (x) .
82. Используя результат предыдущей задачи, покажите, что бифуркация
m= -1
на «языке» двукратно проитерированной функции
F ( x ) =
f ( f ( x ))
от-
вечает бифуркации вилки. Изобразите трансформации функции F(x) для прямой и обратной такой бифуркации. Когда происходит бифуркация удвоения перио- да, а когда жесткий переход через –1? Что можно сказать о знаке производной Шварца в этих ситуациях?
Решение 82. Полученные выше соотношения позволяют утверждать, что
на «языке» двукратно проитерированного отображения
F (x) =
f ( f (x))
наблю-
дается бифуркация «вилка» в том случае, когда в исходном отображении про-
n n
исходит бифуркация m = -1. Действительно, пусть xn = x + x~ , где
x~ – малая
величина. Тогда в окрестности неподвижной точки, используя разложение в ряд Тейлора, имеем
x~ =
F ¢(x) ×
x~
+ 1 F ¢ (x) ×
x~2 +
1 F ¢¢(x) ×
x~3 +
...
![]()
![]()
n+1
n 2 n 6 n
Но, используя установленные свойства производных функции труда получаем:
F (x) , без
![]()
x~ = x~ +
1 F ¢¢(x) ×
x~3 +
...
n+1 n 6 n
Таким образом, мы действительно имеем ситуацию, отвечающую бифур- кации «вилка». Ее появление говорит о наличии некоторой «скрытой» симмет- рии для двукратно проитерированной функции. (Мы говорим о скрытой сим- метрии, поскольку по виду исходной функции ее было бы трудно предполо- жить.)
Бифуркация «вилка» для двукратно проитерированной функции может быть прямой или обратной, в зависимости от знака производной Шварца. Если
производная Шварца
отрицательна Sf
< 0 , то имеет место прямая бифуркация.
В этом случае в терминах исходного отображения наблюдается бифуркация уд-
воения периода. Если же производная Шварца положительна
Sf > 0 , то для
двукратно проитерированной функции имеем обратную
бифуркацию «вилка». Эту бифуркацию можно назвать обратной (субкритической)
бифуркацией уд- воения периода. Ее еще называют
жестким переходом через мультипликатор
m = -1. Такое название связано с тем, что при потере устойчивости неподвиж-
ной точкой по этому «сценарию», изображающая точка обычно перебрасывает- ся на другой аттрактор системы или убегает на бесконечность.
83. Возможен ли жесткий
переход через мультипликатор m = -1 для непод-
вижной точки в логистическом отображении?
Решение 83. Для логистического отображения производная Шварца отри- цательна, и поэтому такая бифуркация неподвижной точки невозможна.
84. Найдите производную
Шварца для функции
f ( x) = a +
bx ±
x3,
соответ-
ствующей кубическому отображению, в точке m = -1. О чем говорят результаты вычислений?
Решение 84. В этом случае
Sf (x) =
f ¢¢(x) - 3
æ
ç![]()
f ¢(x) 2 è
f ¢ (x) ö2
ø![]()
f ¢(x) ÷
= - f ¢¢(x) -
3 [ f ¢ (x)]2 .
![]() 2
2
Для третьей производной в анализируемом случае
f ¢¢(x) = ±6 . Таким обра-
зом, в случае нижнего знака возможен жесткий переход через мультипликатор
- 1. Для верхнего знака производная Шварца отрицательна, и будет наблюдать- ся только удвоение периода.
85.
Для логистического
отображения
xn+1 = 1- lx2
нарисуйте зависимость
n
мультипликаторов неподвижной точки и
2-цикла от параметра на одном графи- ке. Изобразите качественно полный график,
с учетом мультипликаторов 4- цикла, 8-цикла и т.д. Обсудите поведение картины
при приближении к крити-
ческой точке. На графике укажите линию m = +1, а также критическую точку lс
и критическое значение мультипликатора mс .
n![]()
Решение
85. Для логистического отображения торы неподвижной
точки и 2-цикла есть
xn+1 = 1- lx2
мультиплика-
m1 = 1- , m2 = 4 - 4l .
Точки удвоений, в которых мультипликаторы обращается в
-1:
l = 3 и
![]() 1 4
1 4
![]() l = 5 = 1.25 . График
l = 5 = 1.25 . График
2 4
m2 (l)
представляет собой прямую линию с отрицатель-
ным наклоном, рис.59. В пределах окна устойчивости мультипликатор меняется
от + 1 до -1. В других окнах график будет вести себя качественно аналогично,
но с учетом уменьшения размеров окон при приближении к критической точке, наклон будет возрастать. При этом графики будут пересекаться примерно в од- ной точке, тем лучше, чем выше период цикла. В пределе точка пресечения от-
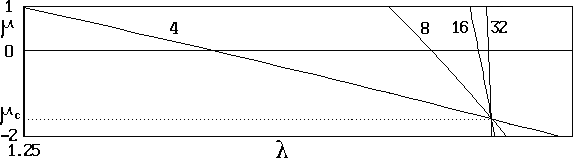 вечает критической точке ликатора mс » -1.60119...
вечает критической точке ликатора mс » -1.60119...
lс = 1.4011552...
и критическому значению мультип-
Рис.59. Зависимость мультипликаторов циклов (период
указан цифрами) от параметра l
вблизи критической точки
86.
Приравняв мультипликатор
неподвижной точки и 2-цикла логистиче- ского отображения, оцените для него
критическую точку и критический муль- типликатор.
Решение 86. Воспользуемся тем свойством, что в критической точке муль-
с![]()
![]()
![]()
типликаторы всех циклов совпадают. Тогда,
приравнивая чаем искомые оценки:
m1 (l) = m2 (l) , полу-
![]() l » 7 + 17
l » 7 + 17
с 8
» 1.39 ,
m » 1-
» -1.562 .
Они достаточно близки к точным.
87.
В таблице представлены
бифуркационные значения параметра, отве- чающие удвоениям периода
логистического отображения. Оцените по этим данным константу dF в законе Фейгенбаума. Оцените наилучшим образом
кри-
тическую точку
lc .
|
ln =0.75 |
|
1.25 |
|
1.36809894 |
|
1.39404616 |
|
1.39963724 |
|
1.40082874 |
Решение 87. По закону Фейгенбаума асимптотически (тем лучше, чем больше период цикла) выполняется соотношение:
![]() ln -
lc
ln -
lc
= d .
F
Отсюда следует, что
ln+1
- lc
![]() ln+1 - ln
ln+1 - ln
= d .
F
ln+2 - ln+1
Лучшее приближение получается, если взять точки трех последних указан-
ных бифуркаций:
dF = 4.6692477. Точное значение dF = 4.669201609…
Из первого соотношения можно получить следующее выражение для кри- тической точки:
l = dFln+2 - ln+1 .
![]()
d F
c -1
Подставляя сюда выражение для константы Фейгенбаума, получаем
lc =
ln+2ln - l2 +1
![]()
n
ln+2 + ln - 2ln+1
= 1.40115346.
Точное значение
lc = 1.401155189...
88.
Для качественного понимания теории
Фейгенбаума можно использо- вать приближенный ренормгрупповой анализ. Для этого выполним отображение
xn+1 =
f (xn ) =
1- lx2
дважды:
f ( f (xn )) , и отбросим члены более высокого по-
n
рядка, чем квадратичный. Тогда заменой
переменной и параметра
f ( f (xn ))
его
можно привести к виду логистического отображения:
Xn+1 = 1- l¢X 2 + ... , где X
n
– перенормированная переменная, а l¢ - новый параметр. Найдите связь новой переменной с x, а также нового значения параметра с величиной l.
Найденная функция
l¢ = j(l)
дает возможность описать каскад бифурка-
ций удвоения и свойства критической точки. Для этого используем, что непод-
вижная точка исходного отображения теряет устойчивость при
l1 = 0.75. Тогда
в точке
l2 , где
l1 = j(l2 ) , будет происходить удвоение неподвижной точки
отображения
f ( f (xn )) , т.е. бифуркация удвоения 2-цикла исходного отображе-
ния. Решая уравнение
l3 = j(l2 ) , получим точку бифуркации 4-цикла и т.д.
Проиллюстрируйте эту процедуру на итерационной диаграмме с помощью гра-
фика
l¢ = j(l). Продемонстрируйте,
что найденная последовательность l
схо-
n
дится к критической точке
lc , и найдите ее приближенное значение. Оцените
масштабный фактор Фейгенбаума aF, отвечающий за перенормировку динами- ческой переменной.
Аппроксимируйте функцию
l¢ = j(l)
касательной вблизи критической
точки, и покажите, что в этом случае точки бифуркаций сходятся к критической
по закону геометрической прогрессии и оцените константу Фейгебаума
dF .
Решение 88. Итерируя логистическое отображение дважды, получаем:
xn+2 = 1- l(1- lx2 )2 = 1- l + 2lx2 - lx4 = 1- l + 2lx2 + ...
n n n n
Заменой переменной x = (1- l) X и параметра l¢ = 2l2 (1- l) оно приводит-
ся к виду параметра
Xn+1 = 1- l¢X 2 . Таким образом, вид функции ренормпреобразования
n
l¢ = j(l) = 2l2 (1- l)
.
Решая уравнения
l1 = j(l2 )
и l3 = j(l2 )
для
l1 = 0.75
находим прибли-
женно бифуркационные значения параметра
l2 = 1.24279 ,
l3 = 1.34400
и т.д.
Процедуру решения иллюстрирует итерационная диаграмма на рис.60.
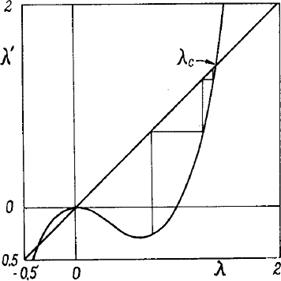
Рис.60. Одномерное отображение, иллюстрирующее
ренормдинамику.
Каскад удвоений сходится к критической точке, для которой
lс = j(lс ) .
Решая это уравнение, находим приближенное значение критической точки
![]()
![]() l = 1+
l = 1+
с 2
3 = 1.36603 .
![]() Теперь находим мультипликатор в критической точке
Теперь находим мультипликатор в критической точке
mс = 1-
= -1.54246. .
Масштабный фактор Фейгенбаума находим из закона перенормировки ди- намической переменной:
aF =
1
![]() 1-
lc
1-
lc
= -2.73205 .
При приближении к критической точке график функции
линейным, так что
j(l)
становится
j(l) = j(lc ) + j¢(lc )(l - lc ) = lc + j¢(lc )(l - lc ) .
Тогда из уравнения для поиска бифуркационных точек
чаем:
ln = j(ln+1 )
полу-
ln = lc + j¢(lc )(ln+1 - lc ) .
Таким образом, накопление точек идет по закону геометрической прогрес- сии, причем
![]() ln - lc
ln - lc
= j¢(l ).
ln+1
- lc
c![]()
Отсюда следует оценка для константы
Фейгенбаума
dF = j¢(lc ) = 4 +
= 5.732.
89.. Придумайте, как можно уточнить вид функции l¢ = j(l).
Решение 89. Для этого можно проитерировать отображение четыре раза и отбросить все члены выше квадратичного:
n
xn+4 = 1- l[(1- l(1- l)2 ]2 + 8l4 (1- l)[1- l(1- l)2 ]x2 + ...
Теперь необходимо пересчитать масштабы так, чтобы это выражение стало эквивалентным двукратно выполненному отображению с параметром l¢ . (Яс- но, что в этом случае мы получим лучшую точность, поскольку начальное при- ближение находится ближе к критической точке). В результате получим:
8l4 (1- l)[1- l(1- l)2 ]{1- [1- l(1- l)2 ]2} = 2(l¢)2 (1- l¢).
Это выражение задает в неявном виде уточненную функцию
l¢ = j(l).
Можно найти критическую точку
lc = j(lc )
и константу Фейгнебаума
dF = j¢(lc )
в этом приближении:
lc = 1.4034) ,
dF = 5.129.
Мы получили значения, заметно более близкие к точным. Отметим, что эту процедуру можно продолжить, т.е. использовать отображение, проитерирован- ное восемь и четыре раза и т.д. В результате будет получаться все более точная
функция
l¢ = j(l)
и критические константы.
90.
Предложите версию приближенного РГ
анализа, использующего свой- ство равенства всех мультипликаторов в критической
точке. Используйте вы- ражения для мультипликаторов неподвижной точки и 2-цикла
логистического отображения.
Решение 90. Условием подобия можно считать равенство соответствую- щих мультипликаторов неподвижной точки и 2-цикла для разных значений па- раметра:
1 2
m (l¢) = m (l)
.
С учетом выражений для мультипликаторов из задачи 85, получаем связь параметров:
.![]()
l¢ = (3 - 4l)2 -1
4
Далее можно полностью следовать логике задачи 88, только с другим ви-
дом функции
l¢ = j(l). В частности, для критической точки и константы Фей-
генбаума получаем:
![]()
![]() l » 7 + 17
l » 7 + 17
с 8
» 1.39 ,
dF = j¢(lc ) = 1+
= 5.123.
91.
![]() Проиллюстрируйте
скейлинг по Фейгенбауму на бифуркационном де- реве для логистического отображения.
Проиллюстрируйте
скейлинг по Фейгенбауму на бифуркационном де- реве для логистического отображения.
Решение 91. Для иллюстрации скейлинга на рис.61 показана окрестность
точки
lc = 1.401152...
во все большем масштабе – каждый выделенный прямо-
угольник дан в увеличенном виде.
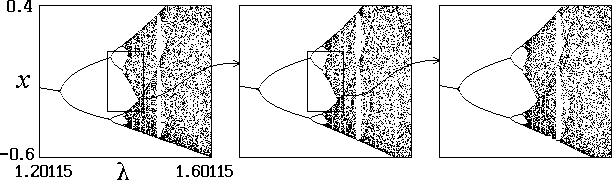
Рис.61.
Скейлинг
на бифуркационном дереве в окрестности критической точки.
При этом масштаб по горизонтальной оси пересчитывается в d=4.6692...
раз относительно критической точки l=lс, а по вертикальной оси x – в
a = -2.5029...
раз (вторая универсальная константа Фейгенбаума) относительно
точки x=0. (Знак минус означает изменение ориентации – картинка переворачи- вается.) В результате получается самоподобная картина.
Бифуркации двухпараметрических одномерных отображений
92.
Для кубического отображения вида
xn+1
= a -
bx 3
найдите область
+ x n n
устойчивости 2-цилка на плоскости
параметров a, b, ограниченную линией
ка- сательной бифуркации и линией удвоения периода неподвижной точки. Пока-
жите, что первая имеет точку сборки. Постройте карту динамических режимов для
данного отображения.
Решение 92. Используя выражение для неподвижной точки отображения
x =
a -
bx +
x3
и приравнивая мультипликатор
m = -b + 3x2 = -1, без труда полу-
чаем выражение для условия удвоения неподвижной точки:
![]()
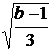 а = ± 2 (2
+ b) .
а = ± 2 (2
+ b) .
3
Обсудим бифуркации 2-цикла. Уравнения для поиска элементов 2-цикла имеют вид:
1
x2=a - bx1
+ x3,
2
x1=a
- bx2 + x3.
Их следует дополнить условием на мультипликатор
m = (-b + 3x2 )(-b + 3x2 ) = ±1.
1 2
В этом случае следует выбирать знак «+» для поиска касательной бифур- кации 2-цикла и знак «–» – для бифуркации удвоения.
Полученные соотношения задают в неявной форме на плоскости (a,b)
систему линий, также показанную на рис.62. На этом рисунке можно видеть, что область устойчивости 2-цикла снизу ограничена линией «предыдущего» удвоения периода. В центре этой области располагается точка сборки, от кото- рой отходят две ветви линии касательной бифуркации. По их «берегам», в свою очередь, идут линии удвоения 2-цикла (рождения 4-цикла), которые проходят мимо точки сборки, приближаясь затем к линии предыдущего удвоения. На ри- сунке серым цветом выделена область бистабильности, внутри которой сосу- ществуют два устойчивых 2-цикла, и изображающая точка может притянуться к какому-то одному из них в зависимости от начальных условий.
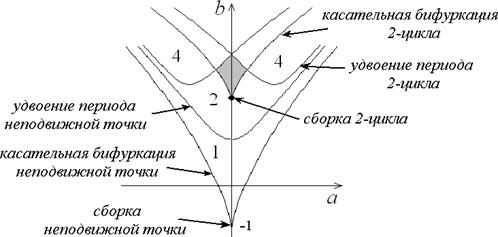
Рис.62.
Бифуркации неподвижной точки и 2-цикла на плоскости параметров; цифрами ука-
зан период цикла. «Crossroad area» –
область существования 2-циклов.
Из рис.62 видно, что область существования 2-цикла имеет на плоскости параметров некоторую характерную форму. Французский математик К. Мира предложил для такой структуры специальное название crossroad area. (В пере- воде с английского – перекресток. Некоторые исследователи называли такие образования «ласточками» из-за их характерной формы.) Эти структуры хоро- шо видны на карте динамических режимов данного отображения на рис.63. На карте разными цветами показаны режимы с разными периодами, белым цветом показаны области хаоса C, а серым – область D убегания траекторий.
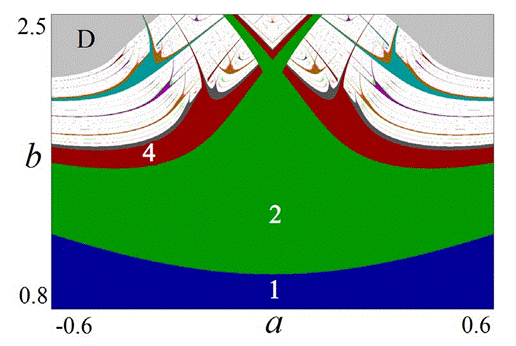
Рис.63.
Карта
динамических режимов кубического отображения
xn+1
= a - bxn
+ x3 .
n
Компьютерное моделирование выявляет типичность таких структур на плоскости
параметров для самых разных отображений. Более того, они могут
возникать на базе циклов всевозможных периодов и образовывать своего рода
+ x
«элементы» в устройстве плоскости параметров.
93. Для кубического отображения
xn+1
= a -
bx 3
на плоскости парамет-
n n
ров найдите линии, отвечающие отображению
максимума в минимум и мини- мума в максимум. Укажите точку на плоскости
параметров, отвечающую 2- циклу, опирающемуся одновременно на два квадратичных
экстремума.
![]() Решение 93. Для этого
отображения максимум и минимум имеют коорди-
Решение 93. Для этого
отображения максимум и минимум имеют коорди-
наты
x1,2 = m
. Условие отображения максимума в минимум имеет вид
x2 =
f (x1)
:
![]()
![]() æ ö
æ ö
= f ç- ÷ ,
è ø
откуда получаем a =
b æ1 - 2 b ö.
![]()
ç ÷
3 3![]()
è ø
Условие отображения минимума в максимум приводит к такому же соот- ношению, но со сменой знака.
Найденные линии пересекаются в точке
![]() a = 0, b = 3 ,
a = 0, b = 3 ,
2
для которой реализуется 2-цкил, опирающийся одновременно на максимум и минимум функции, задающей отображение. Рекомендуем самостоятельно изо- бразить все рассмотренные ситуации на итерационной диаграмме.
94. Покажите, что
двукратно проитерированное отображение
xn+1 =
f (xn )
вдоль линий, отвечающих отображению квадратичного максимума в минимум, характеризуется экстремумом четвертой степени. Что изменит это свойство в характере динамики?
Решение
94. Пусть
x1
– максимум функции, а
x2 – минимум. По условию
x2 =
f (x1) . Разложим функцию в ряд в окрестности точки
x1 :
f (x)
= f (x ) + 1 f ¢ (x )Dx2 + ... = x
![]()
+ 1 f ¢ (x )Dx2 + ...
![]()
1 2 1
В свою очередь
æ 1 ö
2 2 1
è![]()
1 æ 1 ö2
![]() f ( f (x)) =
f ( f (x)) =
f ç x2 +
![]() è 2
è 2
f ¢ (x1)Dx2
+ ...÷ =
1
ø
f (x2 ) + 2
f ¢ (x2 )ç 2
f ¢ (x1)Dx2
+ ...÷
ø
+ ... =
f (x2
) + 1
![]() 8
8
f ¢ (x2
)( f ¢ (x ))2 Dx4
+ ..
В результате вдоль этих линий наблюдаются «нетипичные» удвоения пе- риода, которые не являются Фейгенбаумовскими.
95. Для неподвижной
точки кубического отображения
xn+1
= a + bx
-
x3 :
n n
а) Найдите линию мультипликатора
m = +1
(касательной бифуркации) на
плоскости a, b. Покажите, что эта линия имеет точку сборки, и укажите её ко- ординаты.
б) Найдите линию мультипликатора m = -1 и нанесите её на плоскость a, b.
Вычислите производную Шварца вдоль этой линии и укажите, какие её части отвечают бифуркации удвоения, а какие — жесткому переходу. Укажите на плоскости a, b точку коразмерности два, в которой производная Шварца обра- щается в нуль.
![]() в) Найдите уравнение для линий касательной бифуркации 2-цикла и пока-
жите, что они выходят из найденной выше точки с нулевой производной Швар-
в) Найдите уравнение для линий касательной бифуркации 2-цикла и пока-
жите, что они выходят из найденной выше точки с нулевой производной Швар-
ца и пересекают ось a в точках
a =±
г) Постройте карту динамических режимов.
Решение 95. Обращение мультипликатора в +1 приводит к уравнениям
x = a + bx + x3
, m = b - 3x2 = 1.
Откуда следует, что
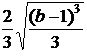 а =
± .
а =
± .
Линии касательной бифуркации, таким образом, сходятся в точке сборки с
координатами
a = 0, b = 1.
Условие обращение мультипликатора в минус единицу приводит к уравнению
m = b - 3x2 = -1
![]()
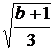 а = ± 2 (2 - b) .
а = ± 2 (2 - b) .
3
Эта линия имеет сложную форму, показанную на рис.64. В частности, она
имеет самопересечение в точке
a = 0, b
= 2
и охватывает точку сборки, пересе-
кая вертикальную ось в точке
a = 0, b = -1.
Вычислим производную Шварца в этом случае. Поскольку
f ¢ (x) = -6x , то
f ¢¢(x) = -6 и
![]() Sf (x) = - f ¢¢(x) - 3 [ f
¢(x)]2 = 6(1- 9x2 ).
Sf (x) = - f ¢¢(x) - 3 [ f
¢(x)]2 = 6(1- 9x2 ).
2
Таким образом, для анализируемого отображения производная Шварца может быть как отрицательной, так и положительной. При этом производная Шварца может изменить знак.
Точки смена знака производной Шварца на плоскости параметров находим
из совместного решения уравнений
1 - 9x2 = 0 ,
m = b - 3x2 =
-1
и соотношения
![]()
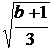 а =
± 2 (2 - b) 3
а =
± 2 (2 - b) 3
. Решая их, получаем:
![]() b = - 2 ,
b = - 2 ,
3
a = ± 16 .
![]() 27
27
На рис.64 эти точки (так же, как и точка сборки) отмечены жирными кружками. Нетрудно показать, что линиям, уходящим от них вверх, отвечает отрицательная производная Шварца, т.е. это линии бифуркации удвоения пе- риода. Отрезок, уходящий вниз и соединяющий эти точки, характеризуется по- ложительной производной Шварца и отвечает жесткому переходу через муль- типликатор m = -1.
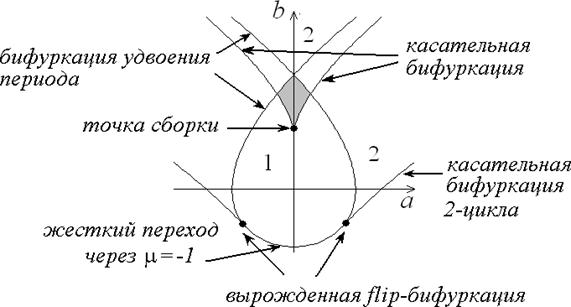
Рис.64. Бифуркации
неподвижной точки на плоскости параметров; цифрами указан период цикла. «Spring area» – область существования неподвижной
точки.
Таким образом, наш анализ выявил новую
бифуркацию коразмерности
два: точку на линии
m = -1, в которой линия удвоения превращается в линию
жесткого переход через мультипликатор
m = -1. Можно показать, что мы уста-
новили не все бифуркационные линии, которые подходят к данной
точке. Область существования устойчивого 2-цикла ограничена снизу линией касательной бифуркации, которая также подходит к исследуемой точке. В па-
раметрической форме она ищется из условия реализации 2-цикла и обращения его мультипликатора в +1:
1
x2=a + bx1
- x3,
2
x1=a
+ bx2 - x3,
m = (b - 3x2 )(b - 3x2 ) = 1.
1 2
Соответствующая линия также показана на рис.63. Заметим, что линия же-
сткого перехода через мультипликатор
m = -1 и линия касательной бифуркации
2-цикла подходят к обсуждаемой точке с одинаковым наклоном. Обсуждаемая бифуркация не имеет в научной литературе строго определенного названия. Один из часто используемых вариантов: вырожденная флип-бифуркация (de- generate flip).
Представленная на рис.64 конфигурация также оказывается типичной при двухпараметрическом анализе различных отображений в случае знакоперемен- ной производной Шварца. Для такой структуры Мира предложил название
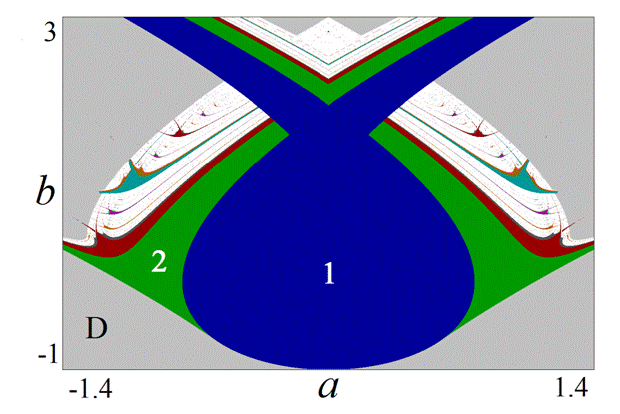
«spring area». Ее
вид на карте динамических режимов иллюстрирует рис.65.
Рис.65.
Карта
динамических режимов кубического отображения
xn+1
= a + bxn
- x3 .
96.
n
Найдите условие, отвечающее существованию кубической точки пере-
гиба для отображения
xn+1
= 1 - ax2
- bx4
- cx
. Какой объект задает это условие
n n n
в пространстве трех параметров a, b, c?
Решение 96. Приравнивая нулю первую и вторые производные, получаем
соответствующее условие:
c = -
4 a .
![]()
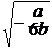 3
3
Это ситуация коразмерности один, ей отвечает поверхность в пространстве трех параметров отображения.
97.
Покажите, что если квадратичный
экстремум отображается в кубиче- скую точку перегиба, то эта ситуация отвечает
«нетипичному» экстремуму функции, задающей отображение, и найдите его порядок.
Решение 97. Решение аналогично задаче 94, реализуется экстремум шес- той степени. Это ситуация коразмерности два и ей отвечает линия в простран- стве трех параметров. То же самое будет для ситуации, когда кубическая точка перегиба отображается в квадратичный экстремум.
98.
Каковы свойства функции, задающей
отображение, при условии, что квадратичный экстремум отображается в другой
квадратичный экстремум, ко- торый отображается в третий такой экстремум?
Решение 98. Функция будет иметь экстремум восьмой степени. Рекомен- дуем самостоятельно изобразить на итерационной диаграмме ситуации из этой и предыдущей задач.
Двумерные отображения и их бифуркации
99.
Изобразите качественно динамику
изображающей точки на фазовой плоскости двумерного отображения непосредственно
в окрестности неподвиж- ной точки в случаях,
когда
·
оба мультипликатора
m1
и m2
действительны и а)
0 < m1
< 1,
0 < m2 < 1;
б) -1 < m1 < 0 ,
0 < m2 < 1; в)
0 < m1
< 1,
-1 < m2 < 0 ; г)
-1
< m1 < 0 ;
-1 < m2 < 0 ;
·
мультипликаторы комплексные, причем модуль близок к
единице, а
фаза – к д) нулю; е)
p / 2 ; ж) p.
Решение 99. Качественные иллюстрации даны на рис.66.
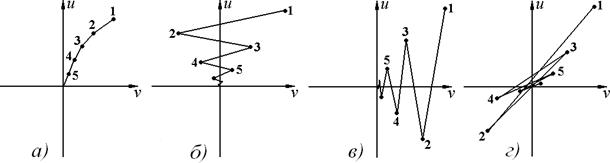
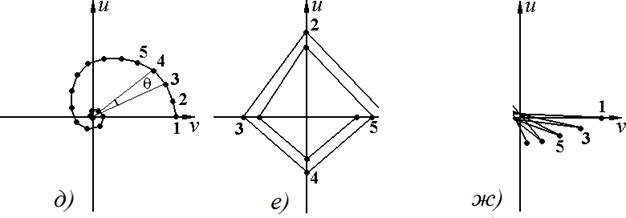
Рис.66. Динамика
в окрестности устойчивой неподвижной точки двумерного отображения. Цифры
означают номер итерации. Верхний ряд отвечает случаю, когда мультипликаторы
действительные, нижний – когда мультипликаторы комплексные.
100.
Выпишите условия для неподвижной
точки произвольного двумерно- го отображения. Получите в общем виде матрицу,
описывающую динамику в окрестности неподвижной точки. Найдите связь между ее
инвариантами – сле- дом и якобианом – с мультипликаторами отображения.
Решение 100. В общем виде двумерное отображение задается с помощью соотношений
xn+1 =
f (xn , yn ),
yn+1 = g(xn , yn ).
Оно может иметь неподвижные точки, которые переходят сами в себя при его однократной итерации. Соответственно, неподвижные точки являются ре- шением следующей системы уравнений:
x0 = f (x0 , y0 ),
y0 = g(x0 , y0 ).
~
Исследуем динамику системы вблизи неподвижной
точки, для чего поло-
жим
хn =
x0 + ~xn и yn =
y0 + ~yn , где
~xn и yn – малые возмущения. Тогда, линеа-
~
ризуя отображение вблизи неподвижной точки,
получаем уравнения, описы-
вающие динамику возмущений ~xn и yn :
~x =
f ¢×
~x + f ¢ × ~y ,
n+1
x n y n
~y =
g¢ × ~x +
g¢ ×
~y .
n+1 x n y× n
Здесь производные вычислены в неподвижной точке. Последние соотно- шения удобно переписать в матричной форме
æ ~x ö æ
~x ö
æ fx¢ f y¢ ö
ç n+1 ÷ = Mˆ ç
n ÷ ,
Mˆ = ç ÷ .
è è è ø ø
ç ~y
÷
n+1 ø
ç ~yn ÷
ç g¢x
g¢y ÷
Матрица Mˆ , составленная из частных производных функций, задающих отображение и вычисленных в неподвижной точке, представляет собой матри- цу Якоби.
Отметим, что для консервативных систем якобиан матицы Mˆ равен еди-
нице:
J = 1. В соответствии со свойствами матриц, условие
J = 1 означает, что
при эволюции любого малого элемента на фазовой плоскости его площадь со- храняется. Для диссипативных систем это не так – они обладают (по крайней мере, локально) свойством сжатия фазового пространства.
Характер устойчивости неподвижной точки определяется свойствами мат- рицы Якоби Mˆ . В рассматриваемом случае она является матрицей «два на два». Такая матрица имеет два собственных числа m1 и m2, которые по опреде- лению и являются мультипликаторами неподвижной точки двумерного ото- бражения. Именно мультипликаторы определяют, устойчива неподвижная точ- ка или нет.
Из свойств матриц следует, что мультипликаторы удовлетворяют следую- щим соотношениям
m1 + m2 = S,
m1 ×m2 = J ,
где S и J – два инварианта матрицы, ее след и якобиан соответственно. Проис- хождение этих двух инвариантов легко понять, если матрица приведена к диа- гональному виду, так что
ˆ æm1 0 ö
M = ç
è 0
÷ .
m2 ø
По определению след – это сумма диагональных элементов такой матрицы, а якобиан для диагональной матрицы равен их произведению.
Далее, по теореме Виета получаем, что мультипликаторы удовлетворяют уравнению:
m2 - Sm + J = 0 .
Это квадратное уравнение, решение которого имеет следующий вид:
m1,2
= S ± .
![]()
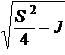 2
2
Таким образом, мультипликаторы неподвижной точки двумерного ото-
бражения могут быть либо действительными, если
S 2 > 4J , либо комплексно-
сопряженными, если двух измерений.
S 2 < 4J . Это новый момент, связанный с существованием
101.
Опишите возможные бифуркации
двумерных отображений на плоско- сти след S
— якобиан J матрицы возмущений.
Укажите область устойчивости неподвижной точки, области, где мультипликаторы
действительные и ком- плексные, а также линии бифуркаций коразмерности один и
точки коразмерно- сти два.
![]()
![]() Решение 101. Граница области устойчивости задается условиями
Решение 101. Граница области устойчивости задается условиями
m = +1 и
m = -1
для действительных мультипликаторов, и
m = 1
–
для комплексных. В
первом случае из соотношения m2 - Sm + J = 0
получаем
1 - S + J = 0 .
Во втором случае, полагая m = -1, получаем 1 + S + J = 0 .
Наконец, третий тип границы отвечает тому, что мультипликаторы непод- вижной точки принимают комплексные значения, а их модуль равен единице.
Мультипликаторы являются комплексными, если
J > S 2 / 4 , и тогда
![]()
![]()
![]() m
= S / 2 ±
i
m
= S / 2 ±
i
. Отсюда легко находим, что
m ×m* = J . Таким образом,
условие
m = 1 означает, что
J = 1.
Все три найденные линии изображены на плоскости параметров (S , J ) на
рис.67. Пересекаясь, они образуют на плоскости параметров треугольник ус- тойчивости неподвижной точки, внутренняя область которого соответствует устойчивой неподвижной точке и показана серым цветом, а внешняя область – неустойчивой. Более темным серым оттенком обозначена область, в которой мультипликаторы принимают комплексные значения. Эта область ограничена
снизу параболой
J = S 2 / 4 .
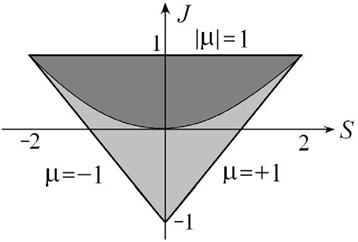
Рис.67.
Треугольник устойчивости неподвижной точки двумерного отображения на плоско-
сти след S - якобиан J матрицы Якоби.
Отметим, что в наших рассуждениях мы фиксировали один из мультипли- каторов, однако, легко найти и второй. Сделаем это, и обсудим поведение мультипликаторов на границах треугольника. Пусть сначала мультипликаторы
действительные. Рассмотрим линию
1 - S + J = 0 . Тогда легко получаем, что
m1 = +1, а m2 = S -1. Таким образом, при движении по плоскости след – якоби-
ан от нижней вершины треугольника к правой вершине вдоль его правой гра- ницы первый мультипликатор остается постоянным и равным +1, а второй из- меняется от –1 до +1.
Аналогично для левой границы треугольника
1 + S + J = 0 , получаем, что
m1 = S +1, а m2 = -1. Следовательно, при движении от нижней вершины тре-
угольника к левой вершине вдоль его левой границы второй мультипликатор остается постоянным и равным –1, а первый изменяется от +1 до –1.
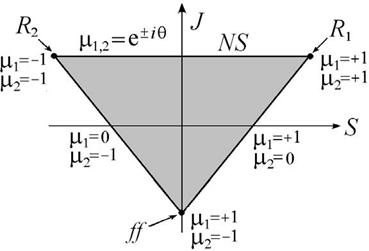
Рис.68. Треугольник
устойчивости на плоскости (S, J).
Обозначены линия бифуркации Ней-
марка-Сакера NS, а также точки коразмерности два: резонанс 1:1
R1 , резонанс 1:2
R2 , точка
fold-flip ff. Указаны значения обоих мультипликаторов
в характерных точках.
Проведенное выше рассмотрение позволяет легко классифицировать про- стейшие бифуркации неподвижных точек двумерного отображения. Границы треугольника устойчивости отвечают бифуркациям коразмерности один, а его вершины – бифуркациям коразмерности два.
Перечислим сначала бифуркации коразмерности один. Две из них извест- ны из анализа одномерных отображений, а третья является новой28.
![]()
28 В скобках даны
другие названия бифуркаций, встречающиеся в литературе.
·
Касательная
бифуркация (fold), m = +1. (Еще один вариант названия –
бифуркация седло-узел.)
Ей отвечает правая граница треугольника на рис.68:
1 - S + J = 0 .
1 + S + J = 0 .
·
Бифуркация
Неймарка-Сакера, J = 1. Это новая бифуркация, характерная
для систем с размерностью фазового пространства два и более. Ей отве- чает верхняя граница треугольника:
J = 1.
Теперь перечислим бифуркации коразмерности два, которым отвечают точки на границе треугольника устойчивости. Они все являются новыми, и не имеют аналогов в теории одномерных отображений. Соответственно, они име- ют свои специальные названия.
·
Резонанс 1:1, R1 . При такой бифуркации оба
мультипликатора обращают-
ся в единицу, m1 = m2 = +1. Условием этой бифуркации является:
S = 2 , J =
1.
·
Резонанс 1:2, R2 . Оба мультипликатора
обращаются в минус единицу,
m1 = m2 = -1. Условие бифуркации имеет вид:
S = -2 , J = 1.
·
Бифуркация fold-flip, ff. Для этой бифуркации m1
= +1, m2
= -1 и
S = 0 , J = -1.
На плоскости инвариантов матрицы Якоби эти бифуркационные точки яв- ляются соответствующими вершинами треугольника, рис.68.
102.
Найдите связь фазы мультипликатора
и следа матрицы линеаризации вдоль линии бифуркации Неймарка-Сакера.
Решение 102. На этой линии мультипликаторы неподвижной точки явля- ются комплексно-сопряженными. В этом случае их удобно записать в виде
m = r × exp(iq) , где r – модуль мультипликатора, а q – его фаза. На этой границе
![]() r = 1, а фаза q будет меняться в зависимости от параметра S. Эту зависимость
r = 1, а фаза q будет меняться в зависимости от параметра S. Эту зависимость
легко найти из соотношения
m =
S / 2 ±
i
, учитывая, что
J = 1. Тогда
для фазы мультипликаторов имеем:
29 Может наблюдаться и
жесткий переход через мультипликатор минус единица.
Отсюда следует, что
tgq = ±
.
![]()
![]() S / 2
S / 2
S = 2 cosq.
В результате при движении вдоль верхней границы треугольника, от его
правой вершины
S = +2
к левой
S = -2 , фаза одного из мультипликаторов бу-
дет меняться от
q = 0
до q = p. Причем, при
S = 0
фаза будет точно равна
![]() q =
p
q =
p
2.
. Отметим, что изменение фазы второго мультипликатора будет проис-
ходить в обратном направлении, т.е. от p до 0.
103.
Изобразите качественно картину
языков Арнольда, примыкающих к этой линии. Где расположены острия резонансных языков с числами вращения
![]()
![]()
![]() 1 , 1
, 1 ?
1 , 1
, 1 ?
3 4 5
Решение 103. Картина языков качественно показана на рис.69. Число вра-
щения w связано с фазой соотношением
q = 2pw . Таким образом,
S = 2 cos 2pw .
Тогда для представленной последовательности получаем значения инварианта
S = - 1, 0,
5 -1.
![]()
![]() 2
2
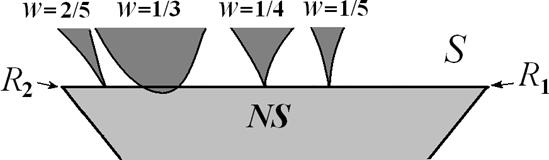
Рис.69. Качественное
расположение основных языков Арнольда вдоль линии бифуркации Неймарка-Сакера
(верхней границы треугольника устойчивости); NS – линия бифуркации
Неймарка-Сакера,
R1 – резонанс 1:1,
R2 - резонанс 1:2, w
– число вращения.
104.
Выпишите все числа вращения,
отвечающие резонансному циклу пе- риода 5. Изобразите качественно все
соответствующие правила обхода элемен- тов цикла.
Решение 104. Для резонансного цикла периода 5 возможны числа враще-
ния
1 , 2 , 3 , 4 . В первом случае траектория «образует» пятиугольник, во втором
![]()
![]()
![]()
![]() 5 5 5 5
5 5 5 5
–
пятиконечную звезду. Третий и четвертый
случаи дают такие же две конфи-
гурации, но с другим правилом обхода элементов, для четвертого случая – вра- щение в противоположном направлении.
105. Есть ли бифуркация
Неймарка-Сакера в отображении Заславского?
Решение
105. Нет,
это отображение с постоянным якобианом.
106.
Найдите диапазон значений параметра
a, в котором является
устойчи- вой нетривиальная неподвижная точка отображения Гукенхеймера и Холмса
xn+1 = yn ,
yn+1 = ayn (1- xn ).
Определите фазовый угол q (аргумент мультипликатора), отвечающий об- ращению якобиана отображения в единицу.
Решение 106. Для нетривиальной неподвижной точки легко находим
y0 = x0
= 1 - 1 . Вычисляем теперь матрицу возмущений в этой точке:
![]() a
a
ˆ æ 0
1 ö æ 0 1ö
M = ç- ay
a(1- x
÷ = ç ÷ .
) 1 - a 1
è 0 0 ø è ø
Таким образом, след и якобиан
S = 1, J
= a . Из «треугольника устойчиво-
сти» легко находим диапазон устойчивости неподвижной точки
0 < a < 1. При-
чем, нижняя граница области отвечает касательной бифуркации, а верхняя –
бифуркации Неймарка-Сакера. В точке этой бифуркации, как известно,
![]() S = 2 cosq. Таким образом, в нашем
случае аргумент мультипликатора q =
p .
S = 2 cosq. Таким образом, в нашем
случае аргумент мультипликатора q =
p .
3
107. Для отображения Эно
n ,
xn+1 = 1 - lx2 - byn ,
yn+1 = xn ,
найдите неподвижные точки, матрицу возмущений, а также её след и якобиан как функции параметров b и l . Найдите линии касательной бифуркации, би- фуркации удвоения периода и нанесите их на плоскость b, l . Укажите также области действительных и комплексных мультипликаторов. Опишите эволю- цию мультипликаторов неподвижной точки отображения Эно на комплексной
плоскости при фиксированном b > 0 при увеличении l .
![]() Решение 107. Неподвижные
точки отображения Эно определяются соот- ношением:
Решение 107. Неподвижные
точки отображения Эно определяются соот- ношением:
x0 = y0 =
- (1+ b) ±
(1+ b)2 + 4l 2l .
Запишем матрицу Якоби. Для этого надо найти соответствующие частные производные, так что в результате получаем:
ˆ æ- 2lx0 -
b ö
M =
ç ÷
.
è 1 0 ø
Перейдем к параметрам след S и якобиан J матрицы Якоби. Для этого след вычисляем как сумму диагональных элементов матрицы, а якобиан – по извест-
ному правилу вычисления определителя. Тогда
S = -2lx0 , J
= b.
Используя вы-
![]() ражение для неподвижной точки, получаем связь следа и якобиана с
исходными параметрами отображения:
ражение для неподвижной точки, получаем связь следа и якобиана с
исходными параметрами отображения:
S = (1+ b) m
J = b.
(1+ b)2 + 4l,
Таким образом,
отображение Эно характеризуется постоянным якобианом.
![]()
![]() Это означает, что оно будет демонстрировать не все описанные выше бифурка-
Это означает, что оно будет демонстрировать не все описанные выше бифурка-
![]()
![]() ции, поскольку условие диссипативности отображения
ции, поскольку условие диссипативности отображения
b < 1
в этом случае оз-
начает
J <
1
и бифуркация Неймарка-Сакера невозможна. В отображении Эно
будут наблюдаться только касательная бифуркация и бифуркация удвоения пе- риода. То есть отображение Эно лишь обобщает уже известные для одномер- ных отображений бифуркации на случай двух измерений. Тем не менее, его би- фуркационный анализ представляет интерес, как пример приложения представ- ленного выше подхода.
Начнем анализ с касательной бифуркации, условие которой задается соот- ношением 1 - S + J = 0 , так что
![]() 1- b -1± + b = 0,
1- b -1± + b = 0,
и после некоторых преобразований приводит к условию
l = - (1 + b)2
![]()
.
4
Будем постепенно увеличивать l, двигаясь по плоскости
(b, l)
вдоль ли-
нии b = const
снизу вверх, рис.70.
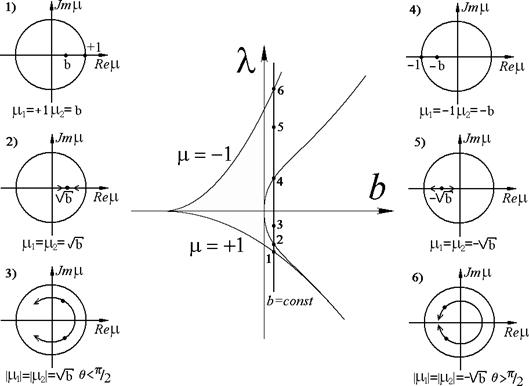
Рис.70. Качественная
эволюция положения мультипликаторов неподвижной точки отобра-
жения Эно
на комплексной плоскости
при движении по плоскости параметров
(b,
l)
вдоль линии
b = const . Цифры
отвечают соответствующим точкам на плоскости парамет- ров.
При
l < -
(1
+ b)2
![]() 4
4
в отображении Эно нет неподвижных точек. Устойчивая
и неустойчивая точки появляются в результате касательной бифуркации. Муль- типликаторы при этом сначала будут оставаться действительными, но при ус-
ловии
S 2 = 4J
сольются на комплексной плоскости и станут комплексно-
сопряженными. Для параметра l этот момент отвечает условию
![]() l =
b - b(1 + b) . Затем мультипликаторы движутся
по окружности радиуса
l =
b - b(1 + b) . Затем мультипликаторы движутся
по окружности радиуса
![]() , обходят начало координат, и снова сливаются при условии
, обходят начало координат, и снова сливаются при условии
![]() l = -b + b (1 + b) .
После чего они опять расходятся вдоль действительной оси.
l = -b + b (1 + b) .
После чего они опять расходятся вдоль действительной оси.
Наконец, при выполнении условия 1 + S + J = 0 , которому отвечает:
3(1 + b)2
![]() l = ,
l = ,
4
один из мультипликаторов обратится в периода.
- 1 и произойдет бифуркация удвоения
Заметим, что для отображений с постоянным якобианом мультипликаторы никогда не обращаются в ноль в силу соотношения m1m2 = J . Это существенное
отличие от случая одномерных отображений. Соответственно, у двумерных отображений не бывает сверхустойчивых циклов. «Наиболее устойчивая» си- туация занимает некоторый диапазон по параметру, отвечающий движению мультипликаторов в комплексной плоскости.
108. Найдите элементы
2-цикла отображения Эно как функции параметров
l и b. Исследуйте устойчивость этого цикла, для чего найдите матрицу возму- щений, вычислите след S и якобиан J этой матрицы. Найдите аналитическое выражение для линии удвоения периода 2-цикла и нанесите ее на b, l плос- кость.
![]() Решение 108. Элементы
2-цикла отображения Эно несложно найти из ис- ходного уравнения
Решение 108. Элементы
2-цикла отображения Эно несложно найти из ис- ходного уравнения
x1,2 =
(1+ b) ± 2
l - 3(1+ b)2 / 4 2l ,
y1,2 = x2,1.
Вычислим матрицу Якоби:
ˆ æ- 2lx2
- b ö æ- 2lx1
- b ö æ 4l2 x1x2 - b
2lx2 ö
M = ç
1
÷
× ç
0 1
÷
= ç
0
÷.
- 2lx -
b
è ø è ø è ø
Откуда получаем выражение для следа и якобиана:
S = 4l2x1x2 - 2b,
J =
b2.
(1+ b)2 - l
![]() Если теперь воспользоваться соотношением x2 x1 = l2
Если теперь воспользоваться соотношением x2 x1 = l2
, то имеем
S = 4(1 + b)2 - 4l - 2b,
J =
b2.
(Отметим, что якобиан можно вычислить и непосредственно из свойств матри-
цы, используя что для произведения матриц
J = J1J2 .)
Определим теперь бифуркации 2-цикла. Очевидно, что касательной би- фуркации 2-цикла отвечает линия удвоения неподвижной точки. Поэтому нам осталось найти линии удвоения периода 2-цикла. Используя соотношение 1 + S + J = 0 , после некоторых преобразований получаем условие удвоения пе- риода для 2-цикла:
l = (1 + b)2 + (1 - b)2 / 4 .
Соответствующие бифуркационные линии на плоскости
(b, l)
показаны на
рис.71. При движении по плоскости этих параметров вдоль линии
b = 0
можно
наблюдать каскад удвоений, отвечающий логистическому отображению.
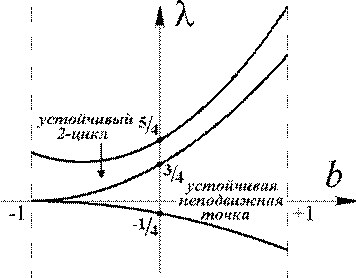
Рис.71. Плоскость (b,l)
отображения Эно и линии простейших бифуркаций.
На рис.72 показана карта динамических режимов отображения Эно, кото- рая дополняет проведенный бифуркационный анализ. На карте можно видеть линии рождения 2- и 4-циклов, подтверждающие аналитическое рассмотрение в рамках бифуркационного анализа, а также области долгопериодических циклов. Внутри области хаоса обнаруживаются структуры типа «crossroad area», кото- рые подробно рассмотрены при анализе одномерных отображений. Две такие структуры, образованные на базе режимов периода 5 и 7, показаны на увели- ченном фрагменте карты.
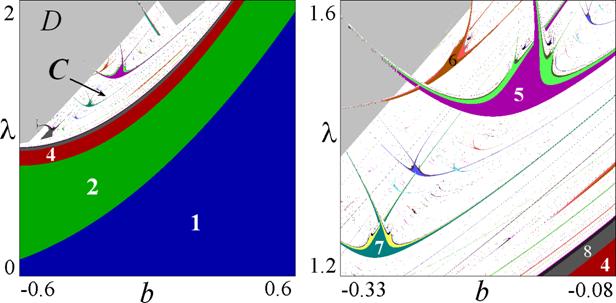
Рис.72. Карта
динамических режимов и ее увеличенный фрагмент для отображения Эно. Цифрами
обозначены периоды режимов, D –
область разбегания траекторий, C– хаос.
109.
Чему равен якобиан N-цикла отображения Эно? Уменьшается или
увеличивается радиус окружности, по которой движутся в комплексной плос- кости
мультипликаторы циклов отображения Эно при удвоениях периода?
Решение 109. Якобиан двумерного отображения отвечает за сжатие эле- ментарной площадки на плоскости динамических переменных. Якобиан непод- вижной точки равен b, а 2-цикла – b2. В силу свойства якобиана матрицы Якоби ясно, что якобиан 4-цикла будет равняться b4 и т.д. Таким образом, с ростом периода циклов якобиан очень быстро стремится к нулю, что на геометриче- ском языке означает сильное сжатие в фазовом пространстве и, фактически, эффективность некоторого одномерного отображения. Соответственно, стре- мится к нулю размер окружности, по которой движутся мультипликаторы в комплексной плоскости.
110.
Для консервативного отображения Эно
опишите эволюцию мультип- ликаторов на комплексной плоскости при удвоениях периода.
Решение 110. На линиях
b = ±1
наблюдается особое поведение, отвечаю-
щее консервативному случаю. В этом случае в отображении нет аттракторов, вместо них в фазовом пространстве наблюдается особый объект – неподвижная точка эллиптического типа, которая с ростом параметра l теряет устойчивость и становится точкой гиперболического типа. При этом в ее окрестности появля- ется 2-цикл эллиптического типа. Если и дальше увеличивать l, то он теряет устойчивость и становится 2-циклом гиперболического типа, а в его окрестно- сти появляется 4-цикл эллиптического типа и т.д. Таким образом, при движении
вдоль линий
b = ±1
имеют место специфические консервативные удвоения пе-
риода. Теория таких систем представляет собой отдельную ветвь нелинейной динамики, поэтому мы не будем здесь подробно останавливаться на этих во- просах.
111.
Дж. Спротт (J. Sprott) предложил
простую модификацию отображения Эно, чтобы бифуркация Неймарка-Сакера стала
возможной30.
Для этого следует просто поменять местами переменные в первом уравнении:
n
xn+1 =
1 - ly2
+ bxn ,
yn+1 = xn .
Спротт называет отображение «минимальным» (minimal 2-D quadratic map), поскольку это практически простейшее по своему виду квадратичное
![]()
отображение с бифуркацией Неймарка-Сакера. Проведите бифуркационный анализ неподвижной точки этого отображения.
![]() Решение 111. Неподвижные
точки отображения Спротта определяются теми же соотношениями, что и для
отображения Эно
Решение 111. Неподвижные
точки отображения Спротта определяются теми же соотношениями, что и для
отображения Эно
x0
Матрица Якоби имеет вид:
= y0
= -
(1+ b) ±
(1+ b)2 + 4l 2l .
ˆ æ b - 2ly0 ö
M =
ç ÷
.
è 1 0 ø
Отсюда легко находим след и якобиан матрицы Якоби, и получаем связь следа и якобиана с исходными параметрами отображения:
![]() S = b,
S = b,
J = 2ly0 = -(1- b) m
(1- b)2 + 4l.
Бифуркацию Неймарка-Сакера находим, приравнивая якобиан единице.
После простых преобразований получаем:
l = 3 - 2b .
![]() 4
4
Концевыми точками для линии бифуркации Неймарка-Сакера являются точки резонанса 1:1 и 1:2. Их находим с помощью соотношений из задачи 101:
·
резонанс 1:1,
·
резонанс 1:2,
b = 2 , l =
-0.25,
b =
-2 , l =
1.75 .
112. Для универсального
двумерного отображения31
n+1 n n n n![]()
x = Sx - y - (x2
+ y2 ),
yn+1
= Jx
- (x2 + y2 ) 5
n n n
покажите, что область устойчивости
тривиальной неподвижной точки имеет вид треугольника из задачи 101. Постройте
карту динамических режимов этого отображения.
Решение 112. Матрица возмущений для тривиальной неподвижной точки имеет вид
ˆ
æ S
M = ç
è J
-1ö
÷ .
0 ø
![]()
31
А.П.
Кузнецов и др. Изв. вузов. Прикладная нелинейная динамика. 2003, №1, с. 12–18.
Таким образом, параметры отображения являются одновременно следом и якобианом матрицы возмущений. Область устойчивости неподвижной точки поэтому дается непосредственно рис.68.
На рис.73 показана построенная численно карта динамических режимов и ее увеличенный фрагмент в окрестности линии бифуркации Неймарка-Сакера.
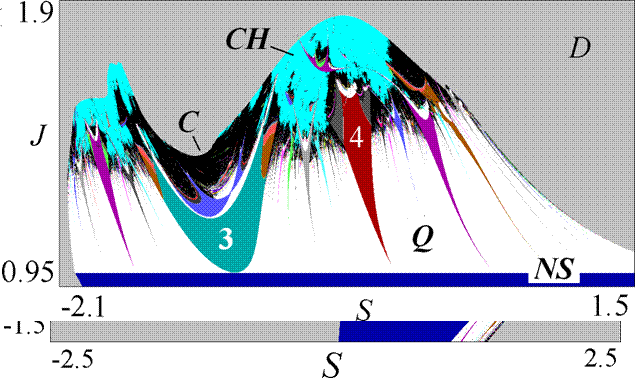
Рис.73. Карта
динамических режимов двумерного универсального отображения и ее увели- ченный
фрагмент в окрестности линии бифуркации Неймарка-Сакера.
Для этого отображения становятся возможными квазипериодические коле- бания, наблюдающиеся выше линии бифуркации Неймарка-Сакера. Для «тра- диционной» карты квазипериодические колебания и хаос неразличимы. Поэто- му рис.73 представляет собой своего рода комбинированную карту режимов и ляпуновских показателей. Здесь, кроме областей с разными периодами циклов, дополнительно хаос С показан черным цветом, а квазипериодические колеба- ния Q – белым. Кроме того, отмечены гиперхаотические режимы CH с двумя положительными показателями Ляпунова, а также D – область разбегания тра- екторий.
Отметим, что линия
m = -1
содержит отрезок, отвечающий удвоению пе-
риода, а также отрезок, отвечающий жесткому переходу через мультипликатор
m = -1. Можно видеть также сложное внутреннее устройство языков синхрони- зации – внутри языков могут иметь место удвоения периода, а также вторичные бифуркации Неймарка-Сакера. При этом «сильные» резонансы имеют свое, ха- рактерное устройство. В этом плане интересно сопоставить языки периода три, четыре и пять.
113. Рассмотрите два
идентичных связанных одномерных отображения
xn+1 =
yn+1 =
f ( xn ) +
e( yn -
xn ) ,
f ( yn ) +
e( xn -
yn ) .
Исследуйте симметричные режимы, т.е. такие, для которых
xn = yn . Пока-
жите, что мультипликаторы неподвижной точки связанных систем даются вы-
ражениями m1 =
f ¢(
x)
и m2 = m1 - 2e . Исходя из этих результатов, найдите линии
касательной бифуркации и бифуркации удвоения периода неподвижной точки на плоскости l , e в случае двух связанных логистических отображений.
Решение 113. Для симметричного режима система редуцируется к одно-
мерной
xn+1 =
f (xn ),
yn = xn .
Найдем матрицу возмущений для анализируемой
системы с учетом симметрии решения:
ˆ æ f ¢(x) -
e
e ö æm
- e e ö
M =
ç e
f ¢(x) - e÷ = ç e m - e÷,
è ø è ø
где m= f ¢(x)
– мультипликатор
индивидуальной системы. Отсюда следует, что
![]() S = 2(m - e), J = (m -
e)2
- e2 . Тогда для двумерного отображения из соотноше-
S = 2(m - e), J = (m -
e)2
- e2 . Тогда для двумерного отображения из соотноше-
ния
m1,2 = S / 2 ± i
следует
m1, = m ,
m2 = m - 2e . Теперь легко находим
условия касательной бифуркации и бифуркации удвоения периода, приравни-
вая
m1,2
= ±1. Для логистического отображения
f ( x) = l- x2
следует использо-
![]() вать m = 1- 1+ 4l , что дает соответствующие линии на плоскости
l , e .
вать m = 1- 1+ 4l , что дает соответствующие линии на плоскости
l , e .
114.
Проведите бифуркационный анализ
неподвижных точек отображе- ния Богданова32
xn+1 = xn + eyn+1,
n
yn+1 = yn + e((m - xn ) yn - a + x2 ).
![]() Решение 114. Неподвижные точки задаются
соотношениями
Решение 114. Неподвижные точки задаются
соотношениями
x0 = ±
a , y = 0.
![]() Верхний знак соответствует всегда неустойчивой точке, так что положим
Верхний знак соответствует всегда неустойчивой точке, так что положим
x0 = -
a. Вычисляя матрицу
возмущений (что рекомендуем проделать само-
стоятельно), получаем:
·
![]() бифуркация Неймарка-Сакера: m = - ,
бифуркация Неймарка-Сакера: m = - ,
·
![]()
![]() касательная бифуркация: a = 0 ,
касательная бифуркация: a = 0 ,
·
бифуркация удвоения периода:
2 + e(
+ m) - e2 = 0,
·
резонанс 1:1:
m = 0,
a = 0 ,
·
резонанс 1:2: m =
-2 / e2
, a = 4 / e4 ,
·
fold-flip: m = -2 / e, a = 0 .
115.
2
Рассмотрим цепочку из емкостей C и индуктивностей L,
показанную на рис.74. Как известно из радиотехники, она представляет собой
фильтр низ-
ких частот. А именно, при условии
w < w0 =
цепочка пропускает сигнал, а
![]() при условии
при условии
w > w0
– нет. Получите
рекуррентное выражение для комплексно-
го импеданса цепочки. Представьте его как двумерное отображение для дейст- вительной и мнимой части соответствующих выражений. Найдите инварианты матрицы возмущений и обсудите вопрос устойчивости неподвижных точек в полосе пропускания фильтра w < w0 .
Решение 115. По правилам параллельного и последовательного соедине- ния получаем рекуррентное соотношение для импеданса цепочки из конечного числа звеньев:
zn+1
= iwL +
zn / iwC .
![]() zn +1/ iwC
zn +1/ iwC
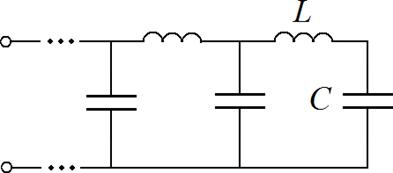
Рис.74. Цепочка из емкостей и индуктивностей.
Далее удобно ввести переменную образований получаем:
xn = 1+ iwСzn . Тогда после простых пре-
xn+1
= d - 1 ,
![]() x
x
где
d = 2 - w2
w2
w![]()
LC = 2 - 2
0
n
– отстройка частоты
от критической. Вводя действи-
тельную и мнимую части переменной, так что
x = x + iy , получаем:
xn+1 = d -
xn ,
![]() x2 + y2
x2 + y2
yn+1 =
n n
![]() yn .
yn .
x2
+ y2
n n
Это и есть искомое отображение. Найдем его неподвижные точки. В пер-
вом случае
y0 = 0 и
d
x![]()
0 = 2 ±
d -1 . Заметим, что по своему определению
2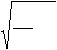
4
d < 2 . Поэтому найденное решение существует при d < -2 . В терминах исход-
0
Поэтому обратимся ко второму случаю, когда
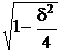 d
d
y0 ¹ 0 . Тогда
x2 + y2 = 1,
так что x = , y =
±
![]()
. Это решение имеет место при
0 0 0 2 0
![]()
33 В этом
случае импеданс цепочки чисто мнимый и стремится к некоторому предельному для
бесконечной цепочки значению.
- 2 < d < 2 . В терминах
исходной системы кания.
w < w0 , что отвечает области пропус-
Вычислим теперь матрицу возмущений. Обращаем внимание, что посколь- ку рассматривается аналитическая функция комплексного переменного, то для уменьшения выкладок можно использовать условия Коши-Римана:
æ x2
- y2 2x y ö
ç 0 0
0 0 ÷
![]()
ç (x2 + y2 )2 (x2 + y2 )2 ÷
M= ç 0 0 0 0 ÷.
2x0 y0 x2 -
y2
![]()
![]()
ç- 0 0 ÷
ç (x2
+ y2 )2 (x2 + y2 )2 ÷
è 0 0 0 0 ø
Тогда для следа и якобиана получаем:
2(x2 - y 2 ) 1
S = 0 0 , J = .
![]()
![]()
(x2 + y 2 )2 (x2
+ y 2 )2
0 0 0 0
В области пропускания
x2 + y2 = 1 и якобиан точно равен единице. Мы
0 0
имеем консервативную ситуацию. Об импедансе бесконечной цепочки в этом случае говорить нельзя – устойчивой неподвижной точки у отображения нет. Рекомендуем самостоятельно построить фазовые портреты для полученного отображения.
Трехмерные отображения и их бифуркации
116.
Для трехмерного отображения в общем
виде укажите условия основ- ных бифуркаций в пространстве инвариантов матрицы возмущений.
Решение 116. В общем виде трехмерное отображение задается следующи- ми соотношениями:
xn+1 =
f (xn , yn , zn ),
yn+1 = g(xn , yn , zn ),
zn+1 = v(xn , yn , zn ).
Оно может иметь неподвижную точку
(x0 , y0 , z0 ) , так что
x0 =
f (x0 , y0 , z0 ),
y0 =
g(x0 , y0 , z0 ),
z0 =
v(x0 , y0, z0 ).
Малые возмущения в окрестности неподвижной точки эволюционируют в соответствии с матрицей Якоби, вычисленной в этой точке:
ç
æ f x¢ f y¢
Mˆ = g¢ g¢
f z¢ ö
÷
¢
ç x y
gz ÷ .
ç v¢ v¢ v¢ ÷
è x y z
ø
Собственные числа матрицы Mˆ являются мультипликаторами отображе- ния, которые определяют характер устойчивости неподвижной точки и отвеча- ют за бифуркации. Для трехмерных отображений матрица Mˆ – это матрица 3´ 3, поэтому уравнение для определения собственных чисел
det(Mˆ - mEˆ) = 0 ,
где Eˆ – единичная матрица, имеет третий порядок.
Матрица Mˆ имеет три собственных числа, и, соответственно, три мульти- пликатора. Поскольку уравнение для определения собственных чисел действи- тельное, то все три мультипликатора могут быть либо действительными числа- ми, либо один из них является действительным, а два оставшихся – комплекс- но-сопряженными. Таким образом, можно сформулировать критерий устойчи- вости: неподвижная точка будет устойчивой, если все мультипликаторы по мо- дулю меньше единицы.
Как и в случае двух измерений, для анализа картины бифуркаций исполь- зуем в качестве параметров инварианты матрицы возмущений. Для этого надо найти связь этих параметров с мультипликаторами. Обозначим мультипликато-
ры через
форме
m1 ,m2 ,m3 . Тогда уравнение третьего порядка может быть записано в
(m - m1)(m - m2 )(m - m3 ) = 0 .
Раскрывая скобки, приходим к соотношению
m3 - Sm2 + Hm - J = 0 , (1)
в котором введены обозначения
S = m1 + m2 + m3 ,
H = m1m2 + m2m3 + m1m,
J =
m1m2m3.
(2)
Величины S, H, J и есть три инварианта матрицы возмущений (матрицы Якоби).
Прежде всего, выясним, как в случае трехмерных отображений представ- лены классические бифуркации, характерные для случаев одного и двух изме- рений. Обсудим их по возрастающей коразмерности.
Сначала найдем условия реализации в трехмерных отображениях извест- ных бифуркаций коразмерности один.
·
Касательная бифуркация
вие этой бифуркации:
m = +1. Подставляя
m = +1 в (1), получаем усло-
H = J -1+ S . (3)
·
Бифуркация m = -1. Подставляя m = -1 в (1), получаем:
H = -J
- 1 - S . (4)
·
Бифуркация Неймарка-Сакера. Условием
бифуркации является обраще- ние в
единицу модуля двух
комплексных
мультипликаторов, так что
m1 = eiq , m2 = e-iq . Подставим эти значения в соотношения (2). Тогда по-
лучим уравнения, содержащие только третий мультипликатор и фазу θ:
S =
2 cosq + m3 ,
H = 2m3 cosq + 1,
J = m3 . (5)
Исключая их, получаем условие бифуркации Неймарка-Сакера:
H = SJ - J 2 +1. (6)
Обсудим теперь бифуркации коразмерности два. Сначала представим би- фуркации, уже известные для двумерных отображений.
·
Резонанс 1:1 R1 . Для этой бифуркации два
мультипликатора обращаются
в единицу:
m1 = +1,
m2 = +1. Подставляя эти соотношения в (2) и исклю-
чая третий мультипликатор, получаем:
S = J + 2 , H = 2J +
1. (7)
·
Резонанс 1:2
R2 . Условием бифуркации являются равенства
m1 = -1,
m2 = -1. Действуя аналогично предыдущему случаю, получаем:
S = J - 2 , H = -2J +
1. (8)
·
Бифуркация fold-flip
ff.
Для этой бифуркации
(2) следует
m1 = +1,
m2 = -1, так что из
S = -J
, H =
-1. (9)
В трехмерной системе появляются также новые бифуркации коразмерно- сти два, обусловленные наличием трех измерений и трех мультипликаторов. Действительно, бифуркация Неймарка-Сакера связана с комплексно- сопряженными мультипликаторами, лежащими на единичной окружности:
m1 = eiq , m2 = e-iq . В трехмерной системе появляется дополнительное условие
устойчивости, связанное с третьим мультипликатором:
-1 < m3 < 1. Таким обра-
зом, возможны новые бифуркации коразмерности два,
когда одновременно вы- полняются условие бифуркации Неймарка-Сакера и условие
обращения в +1 или –1 третьего мультипликатора. В соответствии с этими
условиями, новые бифуркации носят названия фолд-Неймарк-Сакер
(fold-Neimark-Saker) и флип- Неймарк-Сакер (flip-Neimark-Saker).
Найдем условия реализации таких бифуркаций. Поскольку, в соответствии
с третьим уравнением (5)
m3 = J , то равенство
m3 = ±1
приводит к условию
J = ±1. Таким образом, с учетом (6) для новых бифуркаций имеем:
·
Fold-NS:
·
Flip-NS:
H = S ,
H = -S ,
J =
1. (10)
J = -1. (11)
117.
Изобразите границы области
устойчивости неподвижной точки в
про- странстве инвариантов матрицы возмущений.
Решение 117. Чтобы наблюдалась полная картина описанных бифуркаций, система должна характеризоваться тремя существенными параметрами. Рас- смотрим вложение этой картины в пространство инвариантов матрицы возму-
щений (J , S, H ) . Удобство и важность использования такого пространства обу-
словлена тем, что получаемая картина будет, во-первых, полной, а, во-вторых,
универсальной
для
трехмерных отображений.
В пространстве
(J , S, H )
бифуркациям коразмерности один будут отвечать
некоторые поверхности,
а бифуркациям коразмерности два – линии.
Для выяс-
нения структуры пространства
(J , S, H )
построим сначала его сечения плоско-
стями
S = const . Соответствующие иллюстрации для
S = 0 ,
S = 2 и
S = -2
представлены на рис.75. Обсудим их более подробно.
Сечение
S = 0 . В этом сечении на рис.75a можно видеть линию бифурка-
ции Неймарка-Сакера NS, которая в соответствии с (6) представляет собой от-
резок параболы
H = 1- J 2 . Эта линия ограничена двумя новыми точками, ха-
рактерными для
трехмерных отображений: fold-NS ( J
= 1,
H = 0 ) и flip-NS
( J = -1, H = 0 ).
Через эти точки проходят также ограничивающие область устойчивости
линии бифуркаций
m = +1:
H = J -1 и
m = -1:
H = -J - 1. Они, в свою очередь,
пересекаются в точке fold-flip с координатами ( J
= 0 ,
H = -1). Заметим, что ре-
зонансы
R1 и
R2 не попадают в область устойчивости – для них третий мульти-
пликатор оказывается по модулю больше единицы.
Сечение
S = 2 . Сечение
S = 2
показано на рис.75б. В этом случае область
устойчивости ограничена линией бифуркации Неймарка-Сакера, концевыми
точками которой являются точки fold-NS и резонанса ласти устойчивости является линия m = +1.
R1 . Второй границей об-
Сечение
S = -2 . На рис.75в показано сечение
S = -2 . В этом случае отре-
зок линии Неймарка-Сакера ограничен точками flip-NS и резонанса
R2 . Второй
границей области устойчивости является линия мультипликатора m = -1.
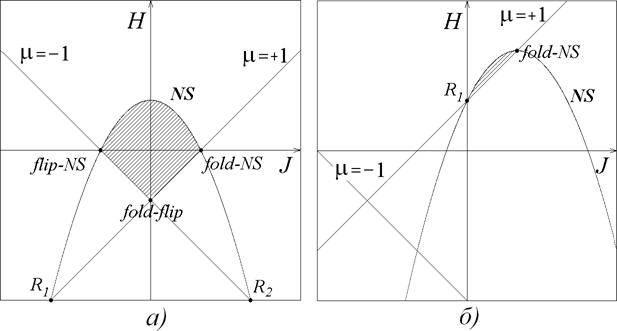
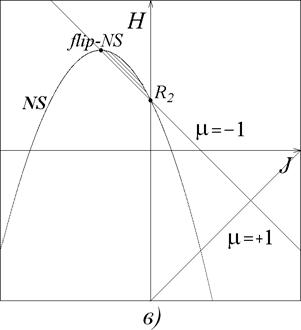 Рис.75. Бифуркационные
линии и бифур- кационные точки трехмерных отображе- ний в сечениях пространства инвариантов
Рис.75. Бифуркационные
линии и бифур- кационные точки трехмерных отображе- ний в сечениях пространства инвариантов
матрицы Якоби
(J , S, H )
плоскостями
S = const : a)
S = 0 , б)
S = 2 , в)
S = -2 .
Область устойчивости неподвижной точки заштрихована.
Таким образом, представленные рисунки иллюстрируют разнообразные возможные и типичные варианты устройства границы области устойчивости неподвижной точки трехмерных отображений. Используя рис.75, можно по- строить картину вложения бифуркаций в трехмерное пространство инвариантов
матрицы возмущений (S, J , H ) , которая показана на рис.76. Как мы уже отме-
чали, в пространстве параметров бифуркациям коразмерности один отвечают некоторые поверхности, а бифуркациям коразмерности два – линии. Возникают и бифуркации коразмерности три, которым соответствуют некоторые точки в пространстве параметров.
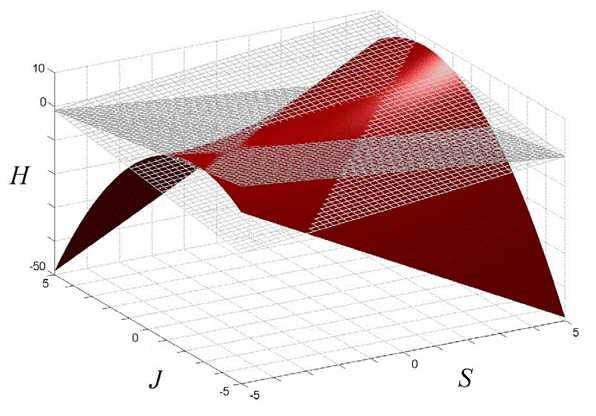
Рис.76. Поверхности
бифуркации Неймарка-Сакера, плоскости мультипликаторов
m = +1 и
m = -1
трехмерных отображений в пространстве инвариантов матрицы возмущений
(J ,
S, H ) .
На рисунке 76 можно видеть следующие поверхности.
· Поверхность H = SJ -
J 2
+1,
которая показана
в цветной графике.
Она
отвечает условию обращения в единицу модуля двух комплексно-сопряженных мультипликаторов.
·
Поверхности
H = J - 1 + S
и H = -J - 1 - S , которые показаны на рисун-
ке в черно-белой графике с нанесенной сеткой координат. Они являются плос- костями в трехмерном пространстве параметров и отвечают условиям обраще- ния одного из мультипликаторов в +1 и –1.
Можно видеть, что за бифуркацию Неймарка-Сакера отвечает лишь часть
поверхности
H = SJ - J 2 +1. Ее устройство удобно исследовать, обратившись к
показанной на рис.77 проекции поверхности бифуркации Неймарка-Сакера на
плоскость (J , S ) .
В соответствии с этим рисунком, в пространстве инвариантов матрицы возмущений бифуркации Неймарка-Сакера отвечает поверхность, ограниченная
линиями
fold-NS, flip-NS, резонансов
R1 и
R2 . Из рис.76 и рис.77 можно видеть,
что имеются также точки новых бифуркаций коразмерности три. Они обозна- чены буквами A и бывают четырех типов.
A1 : m1 = +1, m2 = +1, m3 = -1, общая точка
бифуркаций flip-NS и
R1 .
A2 : m1 = +1, m2 = +1, m3 = +1, общая точка бифуркаций fold -NS и A3 : m1 = +1, m2 = -1, m3 = -1, общая точка
бифуркаций fold -NS и A4 : m1 = -1, m2 = -1, m3 = -1, общая точка бифуркаций flip-NS и
R1 .
R2 .
R2 .
Координаты точек таких бифуркаций в пространстве параметров (J, S, H)
даются соотношениями
A1 (-1, 1, - 1) ;
A2 (1, 3,
3) ;
A3 (1, - 1, - 1) ;
A4 (-1, - 3, 3) .
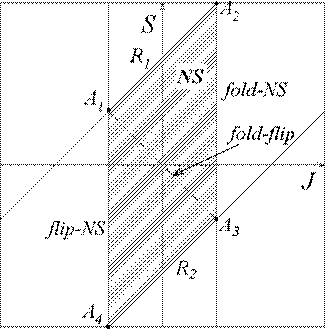
Рис.77.
Проекция
поверхности Неймарка-Сакера NS и
ограничивающих ее линий flip-NS,
fold-NS,
R1 и R2
на плоскость (S, J ) . Пунктир –
проекция линии fold-flip.
В соответствии со свойствами матрицы возмущения, ее якобиан J отвеча- ет за величину диссипации в системе. С ростом якобиана диссипация уменьша-
ется, так что случай
J = 1 отвечает консервативной системе. Поэтому с
физиче-
ской точки зрения важно построить также и сечения пространства параметров
плоскостью
J = const .
Случай
J = 0 . Это очень сильная диссипация, система редуцируется к дву-
мерному отображению. Из уравнений для мультипликаторов (1) получаем, что
m2 - Sm + H = 0 . Таким образом, картине бифуркаций отвечает классический
треугольник устойчивости на плоскости (S, H). Интересно, что при переходе к двумерному отображению роль якобиана играет третий инвариант матрицы возмущений H.
Случай
J = 0.5 . Картине бифуркационных линий и точек отвечает иска-
женный по форме «треугольник устойчивости», показанный на рис.78. При
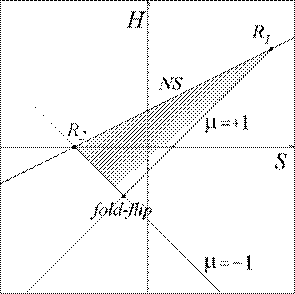
этом линии и точки бифуркаций качественно отвечают случаю
двумерных ото- бражений.
Рис.78.
Бифуркационные
линии и точки трехмерных отображений в сечении пространства
инвариантов матрицы возмущений (J , S, H ) плоскостью J = 0.5 .
Случай
J = 1. Это случай нулевой диссипации, отвечающий переходу к
консервативному пределу. При этом линия Неймарка-Сакера и линия
m = +1 в
соответствии с (3) и (6) даются одним и тем же соотношением
H = S . Таким
образом, эти линии сливаются, и область устойчивости неподвижной точки ис- чезает. Это интересная особенность трехмерных отображений. В двумерных отображениях это не так: при приближении якобиана к единице, область устой-
чивости не стремится к нулю, а заключена в интервале
- 1 < S < 1.
Сечение
H = const . Для полноты картины построим сечение пространства
параметров плоскостью H = 0 . В этом случае бифуркация Неймарка-Сакера (6)
J 2 -1
дается отрезками линии
S = . Бифуркации
![]() J
J
m = +1
отвечает условие
S = 1- J , а бифуркации
m = -1
–
условие
S = -1 - J . Суммарная картина пока-
зана на рис.79. Можно видеть, что одна ветвь линии бифуркации Неймарка-
Сакера ограничена точкой резонанса 1:1
R1 ( J
= -1/ 2 ,
S = 3 / 2 ) и точкой flip-NS
( J = -1,
S = 0 ). Вторая ветвь ограничена точкой резонанса 1:2
R2 ( J = 1/ 2 ,
S = -3 / 2 ) и точкой fold-NS (
J
= 1,
S = 0 ).
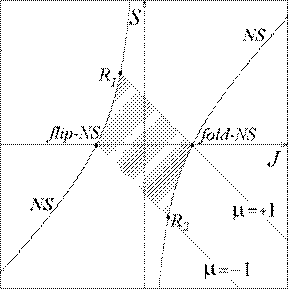
Рис.79. Бифуркационные линии
и точки трехмерных отображений в сечении пространства
инвариантов матрицы возмущений (J , S,
H ) плоскостью H = 0 .
Эно:
118.
Найдите бифуркации неподвижных точек трехмерного отображения
n
xn+1 = a + byn + czn - x2,
yn+1 = xn ,
zn+1 = yn .
Решение 118. Отображение имеет
две неподвижные точки
![]() x0 = y0 = z0 = 2 .
x0 = y0 = z0 = 2 .
Им отвечают разные знаки. Нетрудно показать, что знак минус отвечает всегда неустойчивой точке. Поэтому в дальнейшем оставляем только знак «+».
Матрица возмущений трехмерного отображения Эно выглядит следую- щим образом:
æ- 2x0
b c ö
=
ç
ç
Mˆ ç 1
è 0
÷
÷
0 0÷ .
0
1 ø
Соответственно, получаем уравнение для поиска мультипликаторов:
æ- 2x0 - m b c ö
÷
ç ÷
detç 1 - m 0 = 0 .
ø 0 1 è
ç - m÷
Откуда следует характеристическое уравнение
m3 + 2x0m2 - bm - c = 0 .
![]() С помощью (1) и с учетом выражения для неподвижной точки, находим связь
инвариантов матрицы возмущений с параметрами отображения:
С помощью (1) и с учетом выражения для неподвижной точки, находим связь
инвариантов матрицы возмущений с параметрами отображения:
S = 1 - b -
c -
(1 -
b -
c)2
+ 4a ,
H = -b,
J = с.
Теперь из (3), (4), (5) получаем условия бифуркаций коразмерности один:
·
![]()
![]()
бифуркация Неймарка-Сакера: 4а = 1 + b é1 + b +
1 - 2(b +
c)ù,
c
·
бифуркация m = +1: 4а = -(b + c -1)2
,
ëê c úû
·
бифуркация m = -1: 4а =
4(1 -
b)2
- (b +
c -1)2 , b <
1.
Для бифуркаций коразмерности два из (10), (11) имеем:
·
резонанс 1:1: 4а =
-(2
+ c)2
, b =
-2с - 1,
·
резонанс 1:2:
4а = (6 - 7с)(2 -
с),
b = 2с - 1,
·
fold-flip: 4а = -с2
, b = 1,
·
fold-NS:
4а = -b2
,
с = 1,
·
flip-NS: 4а =
b(3b - 4) , с =
-1, b <
1.
Бифуркации инвариантных кривых (торов)
119. Используя систему Ресслера
x& = - y - z, y& = x + py,
z& = q + (x - r)z,
получите трехмерное отображение, заменив соответствующие производные ко- нечными разностями. Покажите, что в полученном отображении возможна би- фуркация удвоения инвариантной кривой (тора).
Решение 119. Выполним в уравнениях
замену
![]()
![]() dx ® xn+1 - xn ,
dx ® xn+1 - xn ,
dy ®
yn+1 - yn ,
dz ® zn+1 - zn ,
![]()
![]()
![]()
![]() dt h dt h dt h
dt h dt h dt h
где h – параметр дискретизации. Получаем
трехмерное отображение, которое логично назвать дискретным осциллятором Ресслера34:
xn+1 = xn - h( yn + zn ),
yn+1 = yn + h(xn + pyn ),
zn+1 = zn + hq + h(xn - r)zn .
![]()
34 А.Б. Адилова, А.П. Кузнецов, А.В.
Савин. Изв.вузов - Прикладная нелинейная динамика, 2013, №5, с.108.
Обсудим его свойства. На рис.80 приведены примеры портретов аттракторов дискретного осциллятора Ресслера в трехмерном пространстве (x, y, z) для зна-
чения параметра дискретизации
h = 0.1. Из рис.80 можно видеть, что на смену
предельному циклу потоковой системы-прототипа в трехмерном отображении приходит инвариантная кривая. С ростом параметра a эта кривая претерпевает новую бифуркацию, которую называют бифуркацией удвоения инвариантной кривой35. Ее иллюстрирует переход от рис.80а к рис.80б. Это новый тип бифур- каций, который возможен только в трехмерных отображениях (или отображе- ниях более высокой размерности). Соответственно, в потоках, для которых ото- бражение выступает как сечение Пуанкаре, размерность фазового пространства должна быть не менее четырех. При дальнейшем увеличении управляющего параметра происходит эффект потери гладкости удвоенной инвариантной кри- вой, что иллюстрируют рис.80в,г.
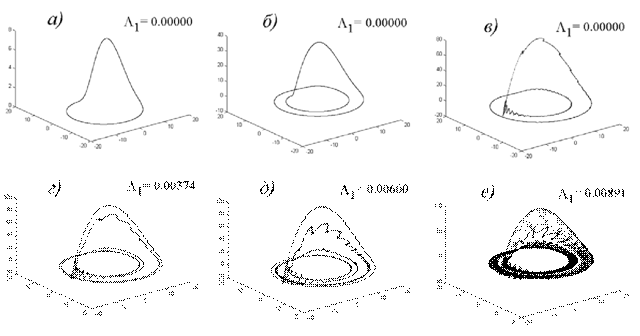
Рис.80. Аттракторы
дискретного осциллятора Ресслера в трехмерном пространстве (x, y, z) ;
h = 0.1, q=0.2, r = 9 . Указано
значение старшего показателя Ляпунова. Значения оставшего-
ся параметра p: а) - 0.02 , б) 0.04 , в)
0.0946 , г) 0.0976 , д) 0.1017 , е) 0.1042 .
Для более детальной характеристики наблюдаемых режимов на всех фраг- ментах рис.80 приведены численные значения старшего ляпуновского показа- теля. Для рис.80а-в он равен нулю, так что наблюдающиеся режимы отвечают квазипериодическим колебаниям. При переходе к рис.80г возникает слабый ха- ос с положительным старшим ляпуновским показателем.
35 Если дискретное отображение
выступает в роли сечения Пуанкаре некоторой потоковой системы, то удвоение
инвариантной кривой отвечает удвоению
тора в такой системе.
Построим график зависимости двух старших показателей Ляпунова от па- раметра a. Такой график представлен на рис.81, причем буквами указаны зна- чения, отвечающие соответствующим фазовым портретам на рис.80. Можно видеть, что случаям а) и б) отвечает нулевой старший показатель. В свою оче- редь, поведение второго показателя дает критерий поиска точки удвоения инва- риантной кривой. А именно, второй ляпуновский показатель в этой точке DT обращается в ноль, оставаясь при других значениях параметра отрицательным.
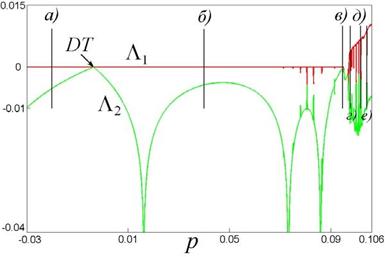
Рис.81.
График
зависимости двух старших показателей Ляпунова L1
и L 2
для дискретного
осциллятора Ресслера от параметра p;
e = 0.1 , q=0.2,
r = 9 . Стрелками и
буквами отмечены
значения, отвечающие рис.79, DT – точка удвоения инвариантной кривой.
120.
Получите дискретное отображение,
соответствующее генератору ква- зипериодических колебаний в форме
0
&x& - (l +
z + x2 - bx4 )x& + w2 x
= 0
z& = b(e - z) - ky2.
Постройте карту ляпуновских показателей на плоскости
(b, l) . Покажите,
что инвариантный тор в системе-прототипе превращается в трехчастотный тор в полученном отображении. С помощью графиков ляпуновских показателей обсудите тип квазипериодических бифуркаций в системе.
Решение 120. Перепишем уравнение в стандартной для динамических сис- тем форме третьего порядка. Заменив производные конечными разностями, по- лучим трехмерное дискретное отображение (тор-отображение)
xn+1 = xn + hyn+1,
yn+1 = yn + h[(l + zn + x2 - bx4 ) yn - w2 x ],
n n 0 n
n
zn+1 = zn + h[b(e - zn ) - ky2 ].
Для первого уравнения, отвечающего скорости изменения переменной x, использована дискретизация по полуявной схеме Эйлера. Карта ляпуновских показателей показана на рис.82. На ней разными цветами показаны: области пе- риодических режимов P (все три показателя отрицательные), область двухчас-
тотных торов
T2
(один показатель нулевой), трехчастотных торов T3
(два пока-
зателя нулевые). Таким образом, для трехмерных отображений (и, соответст- венно, четырехмерных потоков) возможны инвариантные торы разной размер- ности.
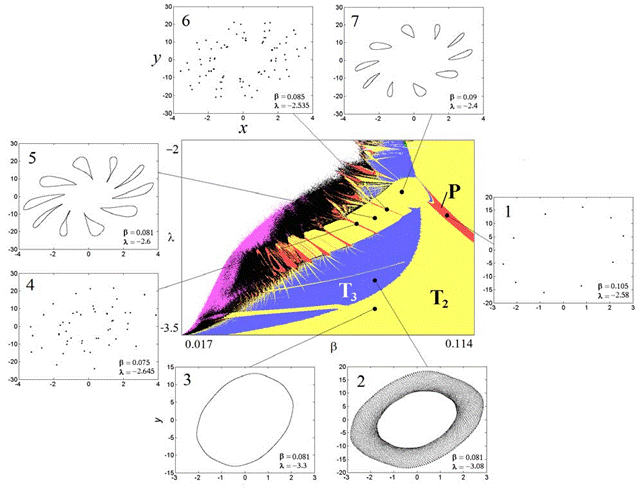
Рис.82. Карта ляпуновских показателей тор-отображения
и характерные фазовые портреты.
По периметру рисунка показаны фазовые портреты в характерных точках. Внутри области P в точке 1 наблюдается резонансный периодический режим с периодом 10. При выходе из этой области в область T2 в точку 3 возникает про- стейшая инвариантная кривая. Если немного увеличить управляющий параметр
l, то инвариантная кривая «размывается» и возникает трехчастотный тор в точ- ке 2. Если же выйти из области P сразу в двухчастотную область в форме ха- рактерной полосы, то возникает резонансный двухчастотный режим в виде де- сяти изолированных инвариантных кривых, точка 7. Внутри этой полосы, в
свою очередь возникают резонансные режимы с очень высокими периодами, точки 4 и 6.
Графики ляпуновских показателей вдоль линии b=0.0465 показаны на рис.83. Они позволяют идентифицировать квазипериодические бифуркации – бифуркации инвариантных кривых (торов). Обсудим их подробнее.
С ростом параметра l в точке QH происходит квазипериодическая бифур- кация Хопфа мягкого рождения трехчастотного тора36. В этом случае имеет ме- сто характерное поведение ляпуновских показателей. Первый показатель все
время остается нулевым:
L1 = 0 , что до порога бифуркации отвечает двухчас-
тотному тору. До порога бифуркации два других показателя совпадают:
L2 = L3
(аналог условия комплексно-сопряженных мультипликаторов). В би-
фуркационной точке показатели
L2 , L3
обращаются в ноль. При дальнейшем
увеличении l показатель L2
область.
остается нулевым, а
L3 уходит в отрицательную
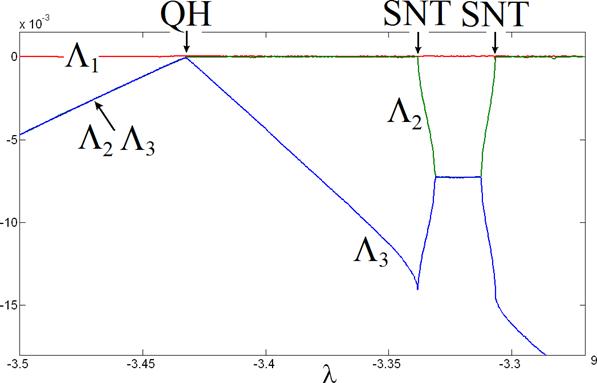
Рис.83. Графики ляпуновских
показателей для тор-отображения при b=0.0465.
В точках SNT наблюдается бифуркация другого типа – седло-узловая би- фуркация торов. На
графике можно видеть окно резонансных двухчастотных
36 Vitolo R., Broer
Н., Simó С. // Regular and Chaotic Dynamics, 2011, № 1–2, p. 154.
торов, ограниченное двумя такими бифуркациями. При выходе через правую
границу показатель L 2
тий же
показатель L3
увеличивается до нуля, а потом остается нулевым. Тре- все время отрицательный. В ходе этой бифуркации ус-
тойчивый двухчастотный тор сталкивается с седловым тором и исчезает, а из общего многообразия возникает аттрактор в виде трехчастотного тора. Левая граница окна образована такой же бифуркацией, но проходимой в обратном по-
рядке. Интересно, что в центре окна
L2 = L3 .
121.
Рассмотрите три связанных
логистических отображения в виде кольца из трех элементов, когда связь содержит
как взаимную, так и одностороннюю компоненты:
n n n
xn+1 = 1- lx2 + e(2xn - yn - zn ) - d(xn - yn ), yn+1 = 1- ly2 + e(2 yn - xn - zn ) - d( yn - zn ), zn+1 = 1- lz2 + e(2zn - xn - yn ) - d(zn - xn ).
Здесь e – регулируемый параметр двусторонней связи, d – постоянная компо- нента односторонней связи. Постройте карты ляпуновских показателей систе-
мы на плоскости
(e,l) , демонстрирующие возможность трехчастотных торов
в системе. Постройте фазовые портреты резонансных двухчастотных торов.
Решение 121. Соответствующие карты представлены на рис.84 для трех значений параметра односторонней связи. Можно видеть характерную систему языков резонансных двухчастотных торов, погруженных в область трехчастот- ных режимов. При этом увеличение параметра удвоений l приводит к расши- рению языков и к возможности хаоса.
На рис.84б показан случай
d = 0.2 . Теперь в левой части рисунка визуали-
зируется характерная резонансная паутина Арнольда: система тонких двухчас- тотных полос, погруженных в трехчастотную область. На пересечении этих по- лос наблюдаются периодические режимы – точные резонансы. При увеличении
параметра до значения
d = 0.3 картина также модифицируется, рис.84в.
Отметим, что серия рисунков 84 в определенной мере иллюстрирует важ- ное свойство квазипериодической бифуркации Хопфа рождения трехчастотного тора: характерная картина режимов зависит не от двух параметров, как для би- фуркации Неймарка-Сакера, а от трех.
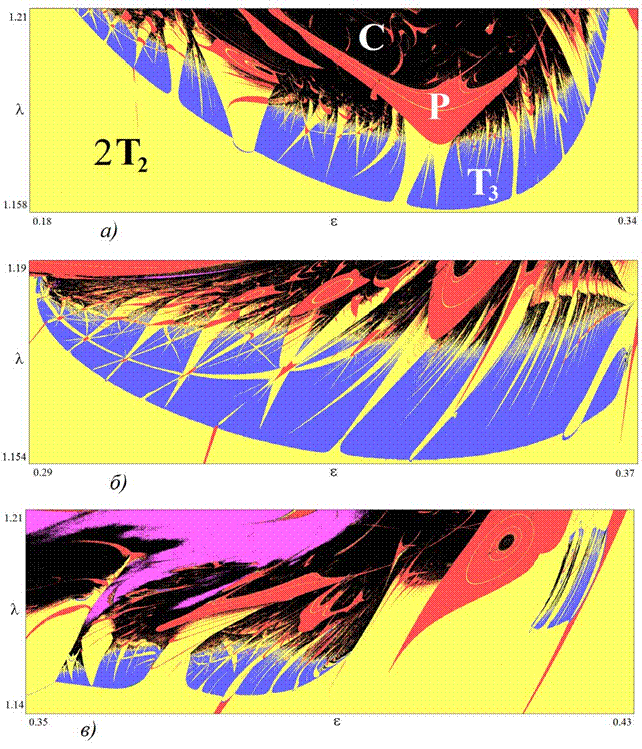
Рис. 84. Карты ляпуновских
показателей трех связанных
логистических отображений, а) d = 0.1 , б) d = 0.2 , в) d = 0.3 .
На рис.85 приведены фазовые портреты торов для двух языков двухчас- тотных режимов рис.84a. Можно видеть, что это сложные инвариантные кри- вые разной формы, возникшие на базе двухкомпонентной инвариантной кри- вой. При этом рис.85а состоит из множества изолированных замкнутых кривых, лежащих на поверхности тора. Рис.85б отвечает двум замкнутым линиям слож- ной формы, также лежащим на поверхности тора.
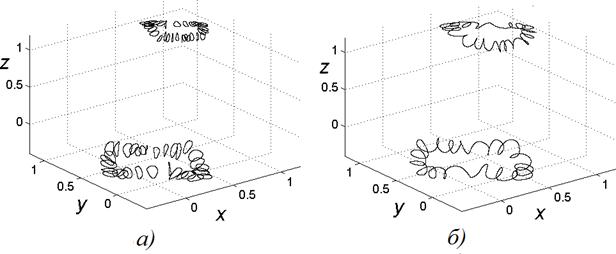
Рис.85. Фазовые
портреты резонансных двухчастотных торов трех связанных логистических
отображений; d = 0.1 , а) e = 0.209 , l = 1.2 , b) e = 0.279 , l = 1.165 .
1.
Эволюция облака изображающих точек
в фазовом пространстве для потоковых систем. Задайте
облако изображающих точек в фазовом простран- стве в виде прямоугольной
«решетки» из набора точек. Напишите программу, позволяющую наблюдать за
эволюцией этого облака во времени для представ- ленных ниже потоковых систем.
Проследите за эволюцией облака. Ответьте на вопросы: консервативна или
диссипативна система? Есть ли в ней аттракторы? Какого типа эти аттракторы?
Проведите компьютерное моделирование для раз- личных значений параметров.
Изменяется ли при этом характер эволюции об- лака? Что происходит с
аттракторами? Попробуйте изменить форму облака и его начальное положение.
Динамические системы для исследования.
· Нелинейный
осциллятор вблизи катастрофы сборки
&x& + gx& + ax + b + x3 = 0 .
·
Уравнение Ван дер
Поля
·
Уравнение Рэлея
&x& - (l- x2 )x& + x = 0 .
&x& - (l- x&2 )x& + x = 0 .
·
Уравнение автогенератора с жестким возбуждением
&x& - (l
+ kx2
- x4
)x& + x = 0 .
·
Брюсселятор
·
Система Ресслера
x& = a - (b +1)x + x2 y, y& = bx - x2 y.
x& = - y - z, y& = x + py,
z& = q + (x - r)z.
2.
Эволюция облака изображающих точек
в фазовом пространстве для отображений. Проведите
исследование, аналогичное описанному в предыду- щей задаче, для представленных
ниже дискретных отображений.
Динамические системы для исследования.
·
Отображение Эно
xn+1
= 1 - lx2 - by ,
n n
yn+1 = xn .
·
Шарик на вибрирующем столе
vn+1 = (1 - e) vn + K sin jn ,
·
Система Икеды
jn+1 = jn + vn+1
(mod 2p).
![]()
![]() 2
2
n
zn+1 = A + Bzn exp(i z ).
·
Отображение Теннисона, Либермана и
Лихтенберга, описывающее отра- жение света от гофрированного зеркала
jn+1 = jn - a sin kxn ,
xn+1 = xn + htgjn+1.
Если система может быть консервативной, особо рассмотрите соответст- вующие значения параметров.
3.
Однопараметрический анализ
потоковых систем. Бифуркация Анд- ронова–Хопфа. Создайте
программу, строящую портреты для представленных ниже динамических систем. Пронаблюдайте
бифуркацию Андронова–Хопфа рождения предельного цикла, его эволюцию при
дальнейшем увеличении пара- метра. Определите порог бифуркации Андронова–Хопфа
из линейного анализа и сравните с результатами компьютерного моделирования.
Динамические системы для исследования.
·
Брюсселятор
x& = a - (b +1)x + x2 y, y& = bx - x2 y.
·
Система, описывающая колебания в гликолизе
x& = 1 - xyg ,
y& = a(xyg - y ).
·
Уравнения колебаний
самолета
j& = r - cosj,
r& = 2r(l - mr - sin j).
·
Модель «хищник–жертва» вида
x& = (a + bx - x2 )x - xy ,
y& = xy - my ,
·
Система Рёсслера
x& = - y - z, y& = x + py,
z& = q + (x - r)z,
при q=2, r=4 и различных p. Для системы Рёсслера постройте как проекции аттракторов на какую-либо координатную плоскость, так и аттракторы в трехмерном пространстве.
·
Генератор Кислова–Дмитриева
Tx& + x = F ( z ),
y& = x - z ,
![]() z& = y - z Q ,
z& = y - z Q ,
где F(z)= Mz
exp(-z2 ) для Q=10 и
T=1.
4.
Двухпараметрическое исследование
двумерных потоковых систем. Постройте плоскость параметров
системы, содержащую аналитически опреде- ленные линии и точки бифуркаций – свои
для каждой динамической системы. Постройте портреты аттракторов (или фазовые
портреты) в выбранных вами точках на плоскости параметров. Проведите
компьютерные эксперименты, ил- люстрирующие динамику системы вблизи линий и
точек бифуркаций, а также внутри характерных областей на плоскости параметров.
Не демонстрирует ли ваша система каких-либо иных бифуркаций, не представленных
на плоскости параметров?
Динамические системы для исследования.
·
Модель «хищник–жертва»
x& = (a + bx - x2 ) x - xy ,
y& = xy - my ,
·
Уравнение типа Ван дер Поля с
нелинейностью, характерной для осцил- лятора с катастрофой складки
&x& - (l - x2 )x& + a + ( x + 1)2 = 0 .
5.
Двухпараметрическое исследование
одномерных отображений. По- стройте карту динамических
режимов одного из предложенных отображений. Линии каких бифуркаций
коразмерности один можно обнаружить на вашей карте? Какие точки бифуркаций
коразмерности два? Укажите ситуации типа “crossroad
area” и “spring area”. Создайте
дополнительную программу, которая строит итерационные диаграммы в задаваемых
вами точках карты. С помощью этой программы проведите следующее исследование:
а) выберите маршрут, пересекающий несколько линий удвоения, и пронаб- людайте каскад удвоений периода на итерационной диаграмме,
в) получите циклы с небольшими периодами, например 3 или 5, в остров- ках устойчивости в области хаоса,
в) выберите точку вблизи линии касательной бифуркации (до ее порога) и пронаблюдайте соответствующую эволюцию изображающей точки,
г) пронаблюдайте хаотические режимы,
д) исследуйте эволюцию аттракторов в окрестности точки сборки,
е) исследуйте эволюцию аттракторов в окрестности flip-бифуркации ко- размерности два.
Просмотрите увеличенные фрагменты карты, внутри которых можно на- блюдать интересную динамику.
Динамические системы
для исследования.
·
Кубическое отображение вида
xn+1
= a - bx
+
x3
.
·
n n
Кубическое отображение вида
xn+1
= a + bx
n n
- x3 .
·
«Квартичное» отображение
x
n+1
= 1 - ax2 - bx4 .
·
n n
Любое другое двух- (и более) параметрическое отображение.
6.
Двухпараметрическое исследование
двумерных отображений. По- стройте карты динамических
режимов двумерного двухпараметрического ото- бражения. Идентифицируйте
бифуркационные линии коразмерности один и точки коразмерности два, а также
характерные композиции бифуркаций на кар- те. «Просмотрите» увеличенные
фрагменты карты, внутри которых можно на- блюдать интересную динамику. Создайте
программу, которая демонстрирует аттракторы отображения. С ее помощью
пронаблюдайте эволюцию аттракторов при вариации параметров, в частности,
каскады удвоений периода, а также хао- тические аттракторы и их эволюцию.
Особое внимание уделите фейгенбаумов- ским критическим аттракторам. Просмотрите
увеличенные фрагменты крити- ческих и хаотических аттракторов. С помощью
программы, демонстрирующей эволюцию изображающей точки на фазовой плоскости,
пронаблюдайте после- довательные «прыжки» этой точки, приближающейся к
неподвижной точке, а также последовательные «прыжки» изображающей точки,
приближающейся к циклу.
Динамические системы для исследования.
·
Отображение Эно
xn+1
= 1 - lx2 - by ,
n n
yn+1 = xn .
·
Шарик на вибрирующем столе
vn+1 = (1 - e)vn + K sin jn ,
·
Система Икеды
jn+1 = j n +vn+1
(mod 2p) .
zn+1
= A + Bzn
exp(i
z 2 ).
·
n![]()
![]()
Отображения «катастроф», отвечающие гиперболической и
эллиптиче- ской омбиликам
xn+1 = xn
+ U x¢ ( x, y )
,
yn+1 = yn + U ¢y ( x, y ).
Здесь потенциальная функция37
U (x, y) = x2 y + y3 /
3 + a( y 2 - x2 )
+ bx + cy
U (x, y) = x 2 y - y 3 /
3 + a( y 2 + x 2 )
+ bx + cy .
Исследуйте характерные сечения пространства параметров при вариации третьего параметра.
7.
Квазипериодические движения и
бифуркация Неймарка-Сакера. По- лучите карты динамических
режимов для представленных ниже систем. Иден- тифицируйте на картах линию
бифуркации Неймарка-Сакера и языки Арноль- да. Постройте портреты аттракторов в
окрестности какого-либо языка. Варьи- руя параметры, пронаблюдайте инвариантную
кривую и резонансный цикл на этой кривой. Пронаблюдайте «прыжки» изображающей
точки, приближающей- ся к инвариантной кривой. Идентифицируйте точки бифуркации
коразмерности два, характерные для двумерных отображений, если они имеются в
вашей сис- теме.
Динамические системы
для исследования.
·
Универсальное двумерное отображение
n+1 n n n n![]()
x = Sx - y - (x2
+ y2 ),
yn+1
= Jx
- (x2
+ y2 ) 5.
·
n n n
Два идентичных логистических отображения с линейной связью
x =l - x2 + e( y - x ),
n+1
n n n
y =l - y2 + e( x - y ).
n+1
n n n
![]()
37
Это
искусственно сконструированные отображения, которые получаются из уравнения
градиентной системы при замене
соответствующих производных на разности типа
xn+1 - xn .
·
n n
Неидентичные связанные логистические отображения с
квадратичной связью
xn+1
= 1 - lx2 - Cy2 ,
n n
для фиксированных B и C.
yn+1
= 1 - Ay2 - Bx2 ,
8.
Неустойчивое и устойчивое
многообразия. Создайте программу, кото- рая строит устойчивое и
неустойчивое многообразия неподвижной точки. Ал- горитм может выглядеть
следующим образом. В очень малой (за пределами разрешения экрана) окрестности
неподвижной точки выбирается случайным образом стартовая точка, которая
подвергается последовательным итерациям. Затем процедура повторяется для другой
стартовой точки и т.д. В результате на экране компьютера прорисуется
неустойчивое многообразие. Чтобы построить устойчивое многообразие, необходимо
реализовать ту же процедуру, итерируя отображение в обратном времени. Для
реализации этого метода необходимо очень точно знать координаты неподвижной
точки. Если она не ищется анали- тически, то предварительно необходимо организовать
соответствующий чис- ленный поиск с помощью метода Ньютона. Пронаблюдайте
трансформацию многообразий при вариации параметров. Зафиксируйте момент
образования гомоклинической структуры и пронаблюдайте ее эволюцию. Исследуйте
две системы: дискретное отображение и поток, причем в последнем случае исполь-
зуйте результаты решения предыдущей задачи.
Дискретные отображения:
·
Отображение Эно
xn+1
= 1 - lx2 - by ,
n n
yn+1 = xn .
·
n n n
Кубическое
отображение типа Эно – отображение Холмса
xn+1
= a - bx
+
x3
- cy ,
·
Отображение кольца
yn+1 = xn ,
qn+1 = qn + W - k sin qn + brn ,
rn+1 = brn - k sin qn .
9.
Бифуркации трехмерных потоков.
Напишите программу, которая
вы-
числяет корни кубического уравнения
g3 -Sg2 + Hg - J
= 0,
коэффициенты кото-
рого являются инвариантами матрицы возмущений. Затем определяется тип со- стояния равновесия по характеру положения корней в комплексной плоскости и
окрашивается плоскость параметров в разные цвета, в соответствии с класси- фикацией равновесий. Постройте разные сечения пространства параметров
10.
Бифуркации в Интернете.
Используя Интернет, создайте обзор ре- сурсов, дающих возможности для
численного исследования бифуркаций.
11.
Численное
исследование бифуркаций. Используя какую-либо
про-
грамму для численного исследования бифуркаций, проведите бифуркационный анализ универсального двумерного отображения
n+1 n n n n![]()
x = Sx - y - (x2
+ y2 ),
yn+1
= Jx
- (x2
+ y2 ) 5.
n n n
Обратите внимание на особенности
внутреннего устройства языков Ар- нольда. Особенно тщательно изучите языки,
отвечающие основным резонан- сам. Используйте предварительную информацию,
полученную методом карт динамических режимов при решении соответствующей задачи.
1. Кузнецов А.П. Кузнецов С.П. Рыскин
Н.М. Нелинейные колебания. М.: Физматлит, 2006, 292 с.
2. Кузнецов А.П., Савин А.В, Тюрюкина
Л.В. Введение в физику нелинейных отображений. Саратов: Научная
книга, 2010, 134 с.
3. Ланда П.С. Автоколебания
в системах с конечным числом степеней свободы. М.: Наука, 1980, 360 с.
4. Анищенко В.С. Сложные
колебания в простых системах: Механизмы воз- никновения, структура и свойства
динамического хаоса в радиофизиче- ских системах. М.: ЛИБРОКОМ, 2009, 320 с.
5. Постнов Д.Э. Введение
в динамику итерируемых отображений. Саратов: Изд-во Саратовского университета,
2007, 160 с.
6. Гукенхеймер Дж., Холмс П. Нелинейные
колебания, динамические систе- мы и бифуркации векторных полей. Ижевск: РХД,
2002, 560 с.
7. Кузнецов С.П. Динамический хаос. М.:
Физматлит, 2006, 356 с.
8. Meijer
H.G.E. Codimension 2 bifurcations of
iterated maps // Doctoral thesis Utrecht University. Адрес в Интернете:
http://igitur-archive.library.uu.nl/dissertations/2006-1204-200716/index.htm.
9. Шильников Л.П., Шильников А.Л., Тураев Д.В. Методы
качественной тео- рии в нелинейной динамике. Москва-Ижевск: ИКИ, . 2003, 442 с.
10.Шильников Л.П., Шильников А.Л.,
Тураев Д.В, Л.Чуа. Методы качествен- ной теории в нелинейной динамике.
Часть 2. Москва-Ижевск: ИКИ, 2009, 548 с.
11. Некоркин В.И. Лекции
по основам теории колебаний. Нижний Новгород: Нижегородский университет, 2012,
311 с.
Учебно-научное издание
Кузнецов Александр Петрович
Динамические системы и бифуркации
![]() Пособие издано в авторской редакции Ответственный за выпуск
А.П.Кузнецов Подписано в печать 19.03.2015 г.
Пособие издано в авторской редакции Ответственный за выпуск
А.П.Кузнецов Подписано в печать 19.03.2015 г.
Формат 60x84 1/16. Бумага Снегурочка. Гарнитура Times New Roman.
![]()
Усл. печ. л. 9,6. Тираж 100 экз.
ООО Издательский центр «Наука» 410600, г. Саратов, ул. Пугачевская, д.117, кв. 50.